Uzasadnienie Miły: Dane są liczby wymierne a,b,c takie, że równanie 2 ax + bx + c = 0 ma dwa rozwiązania rzeczywiste. Uzasadnij, że jeżeli jeden z pierwiastków tego równania jest liczbą wymierną to drugi pierwiastek też jest liczbą wymierną. Proszę o pomoc i wytłumaczenie jak zadanko zrobić. Z góry dziękuję

Basia: równanie liniowe nigdy nie ma dwóch rozwiązań popraw treść

Miły: Zadanie jest wzięte z zadania.info więc nie ma tu błędu.

Miły: aaa, sorka, już widzę gdzie jest błąd

Basia: podaj link

Miły: Dane są liczby wymierne a,b,c takie, że równanie ax² + bx + c = 0 ma dwa rozwiązania rzeczywiste. Uzasadnij, że jeżeli jeden z pierwiastków tego równania jest liczbą wymierną to drugi pierwiastek też jest liczbą wymierną.

Basia: a≠0 a,b,c∊W x₁, x₂ rozwiązania ⇒ ax²+bx+c = a(x−x₁)(x−x₂) = a(x²−x₂*x − x₁*x + x₁*x₂) = ax² − a(x₁+x₂)x + a*x₁*x₂ stąd −a(x₁+x₂) = b

	b
x1+x2 = −		∊ W
	a

	b
jeżeli x1∊W ⇒ x2 = −x1−		∊W
	a

i odwrotnie

Miły: Dzięki

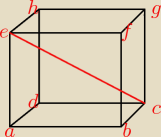
Linka0094: Dany jest sześcian ABCDEFGH, w którym |AB|=3. Oblicz odległość wierzchołka A od przekątnej EC.

Linka0094: sory, że tutaj, ale dalej nie ogarniam tej strony. Z góry dzięki za pomoc