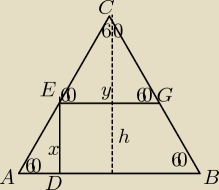
sprawdzenie zadania Alicja: Z dowolnie wybranego punktu na boku trójkąta równobocznego prowadzimy odcinki prostopadłe do dwóch boków. Wykaż, że suma ich długości równa się wysokości trójkąta. Z rysunku wynika że Δ ADE jest podobny do Δ AFC, a Δ ABC jest podobny do Δ CEG Na przeciwko kąta 60^o jest dł. x i h (wierzchołek EAD), a na przeciwko kąta 60^o (wierzchołek ECG) jest dł. y, x jest dwa razy mniejsze od h i teraz jak na podstawie rysunku napisać że x+y=h Wiem że mogę to rozwiązać licząc, że

	ax		ay		ah
Pole ADF+ Pole CEG= Pole ABC =>		+		=		=> ax+ay=ah /:a => x+y=h
	2		2		2

Noi wyszło ale jak to rozwiązać bez liczenia, czy wystarczy wskazać że trójkąt CEG jest równoboczny i te inne podobne?

Alicja: Kurczę przepraszam całe zadanie źle bo przyjełam że jedna prosta jest równoległa, a przeciez dwie są prostopadłe

Alicja:

	1
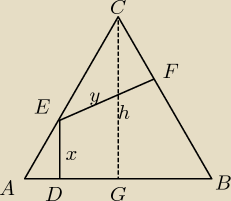
trójkąt ADE jest podobny do AGC więc x=		h
	2

AROB:

	1
Alicjo, skąd wzięłaś związek x=		h , skoro punkt E nie jest środkiem boku AC, lecz
	2

dowolnym punktem?

Eta: Podpowiadam dorysuj odcinek EB otrzymasz dwa trójkąty o polach:

	a*x
P(AEB) =
	2

	a*y
P(BEC =
	2

P(AEB) + P(BEC) = P(ABC) to :

	a*x		a*y		a*h
		+		=
	2		2		2

dokończ..... i otrzymasz: x + y = h

Eta: Alicjo rozumiesz już teraz to zadanie?

Alicja:

	1
Tak rozumiem dziekuję Ja wtedy przyjełam że trójkąt ADE jest podobny do AGC stad x=		h
	2

AS: Oznaczenia przyjąłem jak na rysunku

x		√3
	= sin(60o) ⇒ x = AC*sin(60o) = AC*
AC		2

y		√3
	= sin(60o) ⇒ y = EC*sin(60o) = EC*
EC		2

	√3		√3		√3
x + y = AC*		+ EC*		= (AC + EC)*
	2		2		2

ale AC + EC = AC = a stąd

	a*√3
x + y =		= h
	2