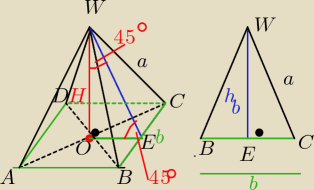
 ΔOEW jest połową kwadratu o boku b2
więc H=b2
to hb = d −−− przekatnej tego kwadratu
czyli hb = b2*√2
teraz z trójkąta po prawej stronie możemy wyznaczyć długość b
z tw. Pitagorasa
IWEI2 + IECI2 = ICWI2
(b√22)2 + (b2)2 = a2
b22 +b24 = a2
ΔOEW jest połową kwadratu o boku b2
więc H=b2
to hb = d −−− przekatnej tego kwadratu
czyli hb = b2*√2
teraz z trójkąta po prawej stronie możemy wyznaczyć długość b
z tw. Pitagorasa
IWEI2 + IECI2 = ICWI2
(b√22)2 + (b2)2 = a2
b22 +b24 = a2
| 4a2 | ||
to 3b2 = 4a2 => b2 = | ||
| 3 |
| 2a | 2a√3 | |||
więc: b= | = | |||
| √3 | 3 |
| 2a√3 | ||
Odp: krawędź podstawy tego ostrosłupa jest b = | [ j ] | |
| 3 |