16 kwi 21:10
Ajtek:
Na oko coś pochodna mi się nie podoba.
Cześć
asdf.
Będę za 15 minut
.
16 kwi 21:16
asdf: cześć, nie musi
ale taka jest
16 kwi 21:18
Mila: Dobrze wolfram pokazuje. Dlaczego wyłączyłeś dziedziny (−1)?
(x−1)2≠0⇔x≠1
16 kwi 21:33
Ajtek:
Źle spojrzałem na pochodną, jest ok
.
16 kwi 21:36
Ajtek:
Witaj
Mila. Też o to właśnie chciałem zapytać
.
16 kwi 21:37
asdf: a no tak..czemu ja wyłączylem −1 z dziedziny
?
16 kwi 21:40
Ajtek:
To tak jak za moją pochodną na pierwszy rzut oka.
Najpierw spojrzałem na pochodną, a później w poszukiwaniu pochodnej zerknąłem na funkcję
wyjściową i coś mi nie pasowało
16 kwi 21:43
asdf: a znacie może sposób całkowania metodą monte carlo? (całki oznaczonej), np. w przedziale od 0
do 2pi funkcji
y = sin(x)
16 kwi 21:45
Ajtek:
Nie pomogę w tej metodzie
.
16 kwi 21:48
Trivial:
Z wykresu funkcji sin(x) w przedziale [0,2π] wynik tej całki to 0.
Wybierz jakąś ciekawszą funkcję.
16 kwi 21:56
asdf: mam ciekawszą funkcję, tylko nie wiem jak to zrobić w matlabie? potrafisz?
16 kwi 21:59
Ajtek:
Cześć
Trivial .
16 kwi 22:00
16 kwi 22:07
Trivial:
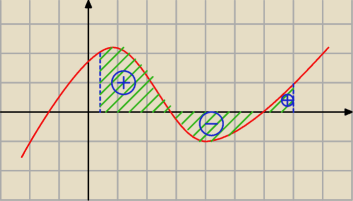
Idea jest taka:
Geometryczna interpretacja całki w przedziale [a,b] z funkcji f(x) to pole wykresu pod funkcją
f(x).
Przesuwa się funkcję f w górę o stałą k, tak żeby nigdzie nie było części pod wykresem.
Nazwijmy powstałą funkcję f
+
Całkujemy funkcję f.
∫
abf(x)dx = ∫
ab(f
+(x) − k)dx = ∫
abf
+(x)dx − k(b−a).
Wybiera się prostokąt, który ogranicza wykres funkcji f
+ w przedziale [a,b].
Liczy się pole prostokąta. Powiedzmy że jest to S.
Aby scałkować funkcję f
+ możemy policzyć jakie jest prawdopodobieństwo p wylosowania punktu
pod wykresem funkcji f
+ i następnie przemnożyć je przez pole ograniczającego prostokąta, w
którym losujemy punkty (S).
∫
abf
+(x)dx = p*S
Prawdopodobieństwo p można policzyć przeprowadzając symulację.
1. Losujemy N punktów postaci (x,y).
2. Liczymy ile z nich spełnia warunek y < f(x). Powiedzmy że jest ich M.
16 kwi 22:15
Trivial: Cześć
Ajtek.
16 kwi 22:15
Trivial: Miało być:
Przesuwa się funkcję f w górę o stałą k, tak żeby nigdzie nie było części pod osią Ox.
16 kwi 22:17
asdf: a mialbys chwile, zeby sprawdzic co jest w tym moim kodzie z wyznacznika nie tak? bufor mi sie
przepelnia i nie wiem jak usunąć pamięć dynamiczną (znam funkcje, wiem gdzie wstawic − ale nie
wychodzi
)
https://join.me/651-797-776
16 kwi 22:19
asdf: albo ewentualnie, moge Ci wyslac ten kod na maila zebyś to zobaczył?
16 kwi 22:23
Trivial: na maila. Na join.me nie wchodzę.
16 kwi 22:25
asdf: na mailu
st****@***.pl, poszlo!
16 kwi 22:38
asdf: doszło?
16 kwi 23:07
Trivial: odpowiedziałem.
16 kwi 23:10
asdf: w ktorej linijce zwalniasz pamięć? i jak? nie ma tutaj funkcji free
16 kwi 23:14
asdf: juz widze gdzie mialem błąd
tablica
odwrocona[i]=(double *)malloc(N*sizeof(double));
tutaj..
a zeby zwolnić pamięć to w mainie na końcu dać free(tablica
bufora bla bla bla?) czy przed
returnem w funkcji wyznacznik?
16 kwi 23:17
asdf: czy w taki sposób:
na koncu w mainie:
for(int i=0;i<N;i++){
free(tablica glowna[i]);
free(tablica odwrocona[i];
}
free(tablica glowna);
free(tablica odwrocona;
na koncu w wyznaczniku − przed return det:
for(int i=0;i<N;i++){
free(tablica wyznacznika bllaa.bla[i]);
}
free(tablica wyznacznika bllaa.bla);
16 kwi 23:22
Trivial: Tak.
16 kwi 23:28
asdf:
for(int i=0;i<N;i++){
for (int j=0;j<N;j++){
tablica
odwrocona[j] [i]=(licz
wyznacznik
macierzy(tablica
glowna,(N−1),i,j))/det
glowny;
}
}
Zrobilem takie cos − od razu transponowaną, tylko mam takie pytanie:
Jezeli jest sobie pamięć, to mniej tak to wygląda?:
A[0]
|| A[1]
|| A[2]
|| A[0][0],A[0][1]A[0][2]
|| A[1][0],A[1][1]A[1][2]
|| A[2][0]A[2][1]A[2][2]
I jeżeli robie zapis od razu:
A[0][0] =...pozniej A[1][0]....A[2][0]
to wychodzą mi takie dziwne rzeczy:
0.60 − ok..
0.00 − nie ok − powinno być 0.10
13771771231237172370000000000000000000000000 − tego juz totalnie nie rozumiem..
pozniej mam:
0.30
0.05
95670340535034400000000000000000000000.00 − znowu ta sama sytuacja
a w ostatniej kolumnie mam:
0.20
0.20
0.20
czyli ostatnia jest ok. Później jak wyświetlam tą tablice o dziwo jest wszystko ok, czyli
liczba 0.00 − zamienia się na 0.10, liczby "miliardowe" są też zamienione na ok..z czego to
wynika?
tutaj jest kod od lini 19 do 46:
http://pastebin.com/LHPgtUPr
17 kwi 00:03
asdf: a może być tak dlatego, że gdy alokuję tą pamięć, to na tych adresach są już jakieś wartości
obok? i one po prostu powiększają tą liczbę, a gdy uzupelniam pozniej pamięć w te brakujące
luki to wszystkie śmieci się usuwają i zastępują się wlasnie tymi uzupelnianymi wartościami?
bo zauważ jest bład przy 0.00, komórka sąsiednia to nie jest 13776556..ona jest oddalona chyba
o 3 pozycje.
17 kwi 00:06
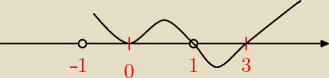Witam
Nie wiem czy to ja zwariowałem, czy wolfram:
jest funkcja: