Odległośc punktu od porostej Mosiarka: Cześć, porzebuję pomocy przy zadaniu z geometrii analitycznej Oblicz odległość punktu C od prostej AB, gdy A= (1,0), B=(3,5), C=(2,7) Co do wzoru ogólnego wyszło mi 3y−4x−7=0 I teraz nie potrafię obliczyć d(C,AB)

Eta: AB: 5x−2y−5=0 więc coś źle policzyłaś C(2,7)

	|2*5−2*7−5|
d(C, AB)=d=		=.........
	√25+4

...: Ja to zrobiłem tak: Prosta AB A=(1,0) B=(3,5) y=ax+b 0=a+b 5=3a+b Przeciwne współczynniki 0=−a−b 5=3a+b 5=2a a=5/2 5=3*(5/2)+b 5=15/2+b 10/2−15/2=b −5/2=b y=5/2x−5/2/*2 wzór prostej : 2y=5x−5 Ax+By+C=0 5x−2y−5=0 (xc;yc)−Współrzędne punktu C |Axc+Byc+C|/pierwiastek(A²+B²) |5*2−2*7−5|/pierwiastek(5²+2²) |10−14−5|/pierwiastek(25+4) |−9|/pierwiastek(29) 9/pierwiastek(29) 9*pierwiastek(29)/29

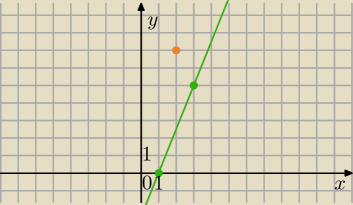
Mila: A= (1,0), B=(3,5), C=(2,7) y=ax+b 0=a+b 5=3a+b ===== 2a=5⇔a=2,5 i b=−2,5 y=2,5x−2,5 do postaci ogólnej: 2,5x−y−2,5=0 /*2 5x−2y−5=0

	|5*2−2*7−5|
d=
	√52+22

Teraz dokończ

Eta:

Eta: AB: y=a_AB(x−x_A)+y_A

	5−0
AB: y=		(x−1)
	3−1

	5
y=		(x−1) /*2
	2

5x−2y−5=0

stanisław:

	Ax0 + By0 + C
d =
	√A2 +B2

	−4 *2 + 3*7 −7
d =
	√−42 +32

	−8 + 21 − 7
d =
	√16 + 9

d = ⁶ _√25 d = ⁶₅ = 1¹₅