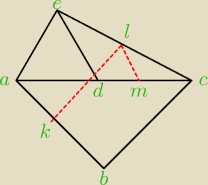
geometria Gość: Trójkąty ABC i ADE są równoboczne (zobacz rysunek). Punkty A ,D i C leżą na jednej prostej. Punkty K ,L i M są środkami odcinków AB ,CE i CD . Wykaż, że ∘ |∡KLM | = 60 .

irena_1: W trójkącie DCE L i M to środki boków, więc odcinek LM jest równoległy do DE, czyli kąt CML ma 120⁰, więc kąt LMA ma 60⁰. W czworokącie ABCE kąty CAE i ACB mają po 60⁰, czyli proste BC i AE są równoległe, czworokąt ABCE to trapez. Punkty K i L to środki ramion trapezu, czyli są do podstaw trapezu równoległe. Stąd kąt MNL ma 60⁰, tyle, co kąt NCB (N to punkt wspólny odcinków AC i KL). W trójkącie NLM więc kąt NLM (więc i kąt KLM) ma 60⁰.

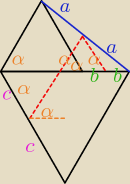
aniabb: z Talesa a/c=a/c więc BC||KL a/b=a/b więc LM||ED 180−2*60=60° =|∡KLM |

Gość: Wielkie dzięki