PROSZĘ O POMOC imielubnick:

	1
rozwiąż równanie 2−2sin22x+sin2x=		, x∊<0,2π>
	2

irena_1:

	1
2−2sin22x+sin2x=		=2−1
	2

−2sin²2x+sin2x=−1 2sin²2x−sin2x−1=0 sin2x=t −1≤t≤1 2t²−t−1=0 Δ=1+8=9

	1−3		1		1+3
t1=		=−		lub t2=		=1
	4		2		4

	1
sin2x=−		lub sin2x=1
	2

	7		11		3
2x=		π+2kπ lub 2x=		π+2kπ lub x=		π+2kπ
	6		6		2

	7		11		3
x=		π+kπ lub x=		π+kπ lub x=		π+kπ
	12		12		4

x∊<0; 2π>

	7		19		11		23		3		7
x∊{		π;		π;		π;		π;		π;		π}
	12		12		12		12		4		4

imielubnick: dziękuję ślicznie ale kurczę, wydawało się trudniejsze mogłem sam zrobić, przepraszam za problem

aniabb: −2sin²2x+sin2x =−1 sin2x=t 2t²−t−1=0 Δ=1+8=9 t=−1/2 lub t=1 sin2x=−1/2 lub sin2x=1 2x=210° lub 2x=330° lub 2x=570° lub 2x=690° lub 2x=270˜° lub 2x=630 x={105,115,135,285,315,345}

Gość: a może mi ktoś wyjaśnić skąd się wzięło 3/4π ?

Gość: tzn chodzi mi o 3/2π ? przepraszam

aniabb: bo sinx=1

aniabb: fakt sinx=1 dla x=π/2

Gość: a czemu to nie jest π/2 ?

aniabb: nie wiem czemu ale myślałam o −1

aniabb: może dlatego że na początku było −1 i jakos tak zostało

Gość: czyli jest błąd tak ? i powinno być że sin2x=π/2 + 2kπ ?

irena_1: A ja też sobie zapisałam, że t₂=−1, nie wiem, dlaczego

	π		5
Ostatnie 2 rozwiązania to {...;		;		π}
	4		4

Gość: to dobrze myślałem, wielki dzięki

irena_1: Gościu! Poprawiłam− zmień ostatnie 2 rozwiązania.

	π		π
Jeśli sin2x=1, to 2x=		+2kπ, czyli x=		+kπ, więc w zadanym przedziale 2 ostatnie
	2		4

rozwiązania to

π		5
	,		π
4		4

imielubnick: heheh, fakt, było źle pod koniec ale ja akurat to od razu ogarnąłem czeski błąd tak zwany

Gość: a może ktoś zechce zrobić jeszcze takie zadanko: W trapezie ABCD o podstawach AB i CD punkt O jest punktem wspólnym przekątnych. Oblicz pole trapezu wiedząc, że pole trójkąta ABO jest równe 5, a pole trójkąta CDO jest równe 4.

aniabb:

h1		√5
	=		⇒ h2=2h1/√5
h2		2

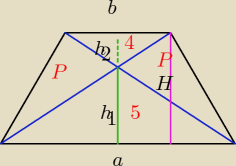
h₁+h₂=H (2/√5+1)h₁ = H //*a/2 (2/√5+1)*ah₁/2 = aH/2 P=(2/√5+1)*5 −5 = 10/√5 = 2√5 Pole trapezu = 9+4√5

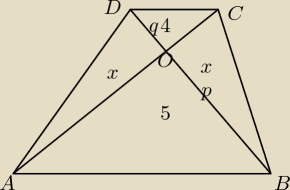
irena_1: Trójkąty ABO i CDO są podobne.

	p
s=		− skala podobieństwa
	q

	5
s2=
	4

	√5
s=
	2

PAOD		q
	=
PABO		p

x		2
	=
5		√5

x=2√5 P_ABCD=5+4+2*2√5=9+4√5

Gość: a mogłabyś dodać komentarz słowny do dwóch ostatnich linijek ? byłbym wdzięczny

aniabb: ah₁/2 to pole trójkąta ABO = 5 aH/2 to pole trójkąta ABC = 5+P

Gość: dzięki już widzę