trygonometria kielbasa
Alois~: wyznacz dziedzinę i zbiór wartości funkcji f(x)=(1−sin
4 x−cos
4 x) / (1−cos
2 x−sin
6 x)
i moje pytanie.. dziedzina juz z wyjsciowego ? czy po przekształceniu.. bo liczac z wyjsciowego
to mi sie nie zgadza z odpowiedzią, wychodzi mi tak :
1−cos
2 x−sin
6 x ≠ 0
sin
2 x − sin
6 x = sin
2 x (1− sin
4 x )
sin
2 x ≠ 0 czyli kπ
k ∊C
sinx≠1 v ≠−1 .. ale w odpowiedziach jest tak :
już nie mówię o dalszej czesci zadania , bo zatrzymałam się juz przy dziedzinie

a do
matury dni.. ?
15 kwi 22:19
MQ: No i dobrze wyszło, bo 1 warunek daje ci x≠kπ, a drugi x≠kπ+π/2
15 kwi 22:32
Alois~: to ja już chyba zgłupiałam całkiem..

bo nie rozumiem

15 kwi 22:37
Saizou : 1−cos
2x−sin
6x≠0
sin
2x+cos
2x−cos
2x−sin
6x≠0
sin
2(1−sin
4x)≠0
sin
2x≠0 lub sin
4x≠1
x≠kπ lub lsinxl≠1
| | 1 | |
czyli mamy powtarzalność co |
| +kπ i taka jest odpowiedź |
| | 2 | |
15 kwi 22:42
Alois~: ale.. to czemu nie ma obydwu odpowiedzi i kπ ? czy to jest to samo..? ale nie no nie jest,
pooolegnee! 
15 kwi 22:43
MQ: No to inaczej:
| | π | |
Z 1 warunku masz sinx≠0 czyli x≠hπ=2h* |
| |
| | 2 | |
| | π | | π | | π | | π | |
Z 2 warunku masz sinx≠1 i ≠−1 czyli x≠hπ+ |
| =2h* |
| + |
| =(2h+1)* |
| |
| | 2 | | 2 | | 2 | | 2 | |
h należy do liczb całkowitych
| | π | |
2h to wszystkie parzyste, czyli w 1 masz wszystkie parzyste razy |
| |
| | 2 | |
| | π | |
2h+1 to wszystkie nieparzyste, czyli w 2 masz wszystkie nieparzyste razy |
| |
| | 2 | |
| | π | |
w sumie masz wszystkie liczby całkowite razy |
| |
| | 2 | |
| | π | |
czyli możesz napisać x≠k* |
| |
| | 2 | |
15 kwi 22:45
Alois~: MQ wieelkie dzięki nie wiem czy załapie ale spr chociaz, a jesli bym zapisała obydwa
wyniki.. jako dziedzine to jest dobrze? w sensie czy uznaja mi na rozszerzeniu
15 kwi 22:52
Saizou :
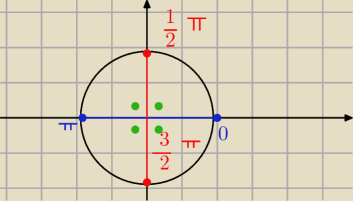
pokażę to na kole trygonometrycznym
−rysujemy koło
− i teraz czary

zaznaczamy kąt
kπ (musimy uwzględnić powtarzalność) dla k=0 mamy 0, dla
k=1 mamy π, dla k=2 mamy 2π (czyli powtarzalność co π)
| | 1 | | 1 | | 3 | |
− to samo dla |
| π+kπ dla k=0 mamy |
| π, dla k=1 mamy |
| π, dla |
| | 2 | | 2 | | 2 | |
| | 1 | |
−czyli koło podzieliło się na 4 równe części, zatem uzyskaliśmy powtarzalność co |
| kπ |
| | 2 | |
15 kwi 22:52
Alois~: Saizou to teraz... już całkiem

ale też dzieki, ja nie wiem co mi sie z glowa dzieje

ze ja tego nie czaje
15 kwi 22:58
Saizou :
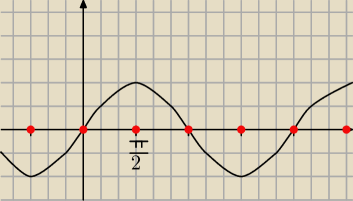
ale metoda koła jest prosta, tylko że ja nie umiem dobrze wytłumaczyć zapewne

można też z wykresu
| | 1 | |
czerwone kropki to co nam wyszło jest zaznaczone i od razu widać że powtarzają się co |
| kπ |
| | 2 | |
15 kwi 23:02
Alois~: ooo ! i teraz załapałam


dzięki
Saizou oświeciłes mnie

ale jak zapisze obydwa rozwiazania w dziedzinie to uznaja mi prawda?

15 kwi 23:05
Saizou : to zależy czy będą chcieli w jak najprostszej postaci czy też nie
15 kwi 23:07
Alois~: a zbior wartosci jak tutaj okreslic wyliczyc do najprostszej postaci i.. ?
15 kwi 23:09
MQ: Myślę, że tak.
15 kwi 23:12
Alois~: zajrze jutro

dobrej nocy życze

15 kwi 23:15
 a do
matury dni.. ?
a do
matury dni.. ?
 bo nie rozumiem
bo nie rozumiem 

 pokażę to na kole trygonometrycznym
−rysujemy koło
− i teraz czary
pokażę to na kole trygonometrycznym
−rysujemy koło
− i teraz czary  zaznaczamy kąt kπ (musimy uwzględnić powtarzalność) dla k=0 mamy 0, dla
k=1 mamy π, dla k=2 mamy 2π (czyli powtarzalność co π)
zaznaczamy kąt kπ (musimy uwzględnić powtarzalność) dla k=0 mamy 0, dla
k=1 mamy π, dla k=2 mamy 2π (czyli powtarzalność co π)
 ale też dzieki, ja nie wiem co mi sie z glowa dzieje
ale też dzieki, ja nie wiem co mi sie z glowa dzieje  ze ja tego nie czaje
ze ja tego nie czaje
 ale metoda koła jest prosta, tylko że ja nie umiem dobrze wytłumaczyć zapewne
ale metoda koła jest prosta, tylko że ja nie umiem dobrze wytłumaczyć zapewne  można też z wykresu
można też z wykresu

 dzięki
Saizou oświeciłes mnie
dzięki
Saizou oświeciłes mnie  ale jak zapisze obydwa rozwiazania w dziedzinie to uznaja mi prawda?
ale jak zapisze obydwa rozwiazania w dziedzinie to uznaja mi prawda? 
 dobrej nocy życze
dobrej nocy życze 