Wyznacz współrzedne D Tina: Punkty A=(−2,3), B(1,2) i C(2,−1) są kolejnymi wierzchołkami rombu ABCD. Wyznacz współrzędne wierzchołka D... Błagam o wskazanie co robię źle i dlaczego tak nie można bo już któryś z kolei mi się to zeruje...ale do rzeczy, zaczęłam to robić tak: Długość odcinka |AC|=√10 Równanie prostej AB

	1		7
y=−		x+
	3		3

Równanie prostej równoległe do tej prostej czyli CD:

	1		1
y=−		x −
	3		3

	1		1
Z tego wiem, że punkt D ma współrzędne (x, −		x −		) <−−− czy tu leży problem?
	3		3

Równanie ogólnej prostej CD x+3y+1=0

	1		1
I teraz odległość punktu D(x, −		x −		) od prostej x+3y+1=0 wynosi √10
	3		3

Czyli

	1   1   |x+3(− x − )+1|   3   3
√10 =
	√10

	|x−x −1+1|
√10=		(jakie powinny być współrzędne punktu D żeby nawias się nie
	√10

zerował? tu leży problem? mam tak już któryś raz i dalej nie wiem gdzie leżał problem...

MQ: Po co tak skomplikowanie to robisz? Użyj wektorów. Skoro to romb, to AD^→=BC^→ BC^→=[2−1,−1−2]=[1,−3] AD^→=[x_D−(−2),y_D−3]=[1,−3] stąd: x_D−(−2)=1 y_D−3=−3 stąd x_D=−1 y_D=0 D=(−1,0)

Saizou : ale ta odległość jest od złej prostej liczona, bo liczysz odległość punktu D od prostej CD, czyli musi wyjść 0 ja polecam do tego zadania wektory np. (piszę bez strzałek nad wektorami) AB=DC [1+2;2−3]=[2−x;−1−y] 3=2−x −1=−1−y x=−1 y=0 D(−1:0)

Saizou : oj sorry, nie zauważyłem że jest już odpowiedź, bo nie odświeżałem strony i miałem jakąś zawiechę przy tej prostej

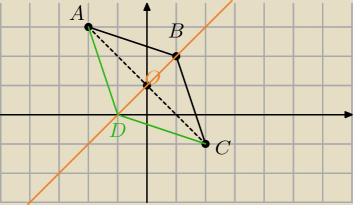
Mila: Korzystasz z własności rombu. Punkty A=(−2,3), B(1,2) i C(2,−1) są kolejnymi wierzchołkami rombu ABCD. Punkt D jest symetryczny do punktu B względem prostej AC. Prosta AC: y=ax+b 3=−2a+b −1=2a+b odejmuję stronami 4=−4a⇔a=−1 i b=1 y=−x+1 DB⊥AC DB: y=x+b i B∊prostej ⇔2=1+b ⇔b=1 y=x+1 Punkt przecięcia x+1=−x+1 x=0 i y=1 O=(0,1) jest środkiem DB D(x,y)

	x+1
0=		⇔x+1=0⇔x=−1
	2

	y+2
1=		⇔y+2=2⇔y=0
	2

D=(−1,0)

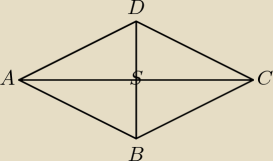
baca: S = (0, 1) D = (x_D, y_D), x_D + 1 = 2*0, x_D = −1, y_D + 2 = 2*1, y_D = 0, D = (−1, 0)

baca: czego was uczą?, chyba nie myślenia.

Tina: Dziękuje bardzo Mila, nie wiem co bym bez Ciebie zrobiła . A co jest nie tak w moim rozumowaniu ? Dlaczego to pod wartością bezwzględną się wyzerowało?

Saizou : obliczyłaś odległość punktu D od prostej CD, więc musiało się wyzerować

Mila: AC to przekątna, odległość punktu D od prostej AB jest równa wysokości rombu.

Mila: Staraj się w geometrii analitycznej zrobić zawsze rysunek, to pomaga.

Tina: @baca. Cieszy mnie, że wszystko umiesz jednak nie każdy wszystko potrafi... Dziękuję Mila, już wszystko jasne

Mila: Powodzenia w dalszych zmaganiach.