Geometria
tcl28: W trójkąt równoramienny ABC, w którym AC=BC, ∡C=120o, wpisano okrąg, którego promień jest
równy 3 cm. Oblicz długość boków trójkąta.
15 kwi 21:16
PW: Poprzez pole − raz liczone jako iloczyn połowy obwodu i promienia okręgu, drugi raz jako połowa
iloczynu długości ramion i sinusa kąta między nimi. Jeszcze jeden związek między ramionami i
trzecim bokiem da tw. cosinusów.
15 kwi 23:57
Eta:
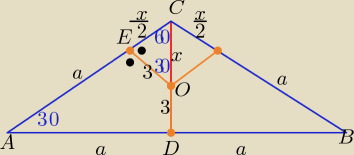
Z trójkątów prostokątnych o kątach 30
o, 60
o, 90
o ( lub z funkcji trygonometrycznych)
z ΔECO:
|OC|=x= 2
√3 , |EC|=
√3 to: |DC|=3+2
√3
podobnie
zΔADC : |AD|=a=(3+2
√3)*
√3= 3(
√3+2) to |AB|=2a=
6(√3+2)
| | x | |
|AC|=|BC|= a+ |
| = 3(√3+2)+√3= 2(2√3+3) |
| | 2 | |
16 kwi 00:36
 Z trójkątów prostokątnych o kątach 30o, 60o, 90o ( lub z funkcji trygonometrycznych)
z ΔECO:
|OC|=x= 2√3 , |EC|=√3 to: |DC|=3+2√3
podobnie
zΔADC : |AD|=a=(3+2√3)*√3= 3(√3+2) to |AB|=2a= 6(√3+2)
Z trójkątów prostokątnych o kątach 30o, 60o, 90o ( lub z funkcji trygonometrycznych)
z ΔECO:
|OC|=x= 2√3 , |EC|=√3 to: |DC|=3+2√3
podobnie
zΔADC : |AD|=a=(3+2√3)*√3= 3(√3+2) to |AB|=2a= 6(√3+2)