matematykaszkolna.pl
zadanie z planimetrii Weronika: W trójkącie ABC dwusieczna kąta ACB przecina bok AB w punkcie P. Wykaż, że APAC=BPBC
15 kwi 18:28
M:
28 gru 13:55
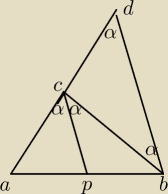
młodziutki: rysunekPoprowadźmy prostą BD równoległą do PC, wtedy ∠BDC = ∠PCA = ∠DBC, ponieważ ∠DCB = 180−2α.
 DC BP BC BP 
Z talesa:
=
, ale skoro DC=BC to
=
. ckd
 AC AP AC AP 
28 gru 14:56
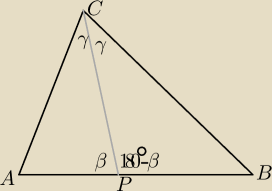NN: rysunek z tw. sinusów w ΔAPC
 AP AC AP*sinβ 
=
⇒ sinγ=
 sinγ sinβ AC 
i z tw. sinusów w ΔPBC
 PB BC PB*sinβ 
=
⇒ sinγ=
 sinγ sinβ BC 
 AP PB 
to
=
 AC BC 
c.n.w.
28 gru 15:06
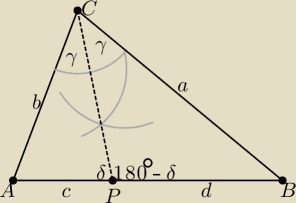
Ykreg: rysunek
 c d 
Teza:
=
 b a 
Dowód: np. z wykorzystaniem twierdzenia sinusów: sin(180o − δ) = sinδ
 b c a d 
w ΔAPC:
=
oraz w ΔPBC:
=
itd.
 sinδ sinγ sinδ sinγ 
28 gru 15:07
NN: emotka
28 gru 15:18
Ykreg:
28 gru 15:24