 0;5]→R, gdzie f(x)=x3+3x2−24x+4, wyznaczyć wartość największą i najmniejszą:
Mój problem w tym zadaniu polega na "niechlujnie" zrobionym. Nie wiem do końca co to znaczy,
ale muszę to zadanie zrobic dobrze. Prosił bym o rozpisanie tego zadania tak aby nie było się
czego przyczepić.
f'(x)=3x2+6x−24
3x2+6x−24=0 //3
3(x2+2x−8)
Δ=22−4*1*(−8)
√Δ=6
0;5]→R, gdzie f(x)=x3+3x2−24x+4, wyznaczyć wartość największą i najmniejszą:
Mój problem w tym zadaniu polega na "niechlujnie" zrobionym. Nie wiem do końca co to znaczy,
ale muszę to zadanie zrobic dobrze. Prosił bym o rozpisanie tego zadania tak aby nie było się
czego przyczepić.
f'(x)=3x2+6x−24
3x2+6x−24=0 //3
3(x2+2x−8)
Δ=22−4*1*(−8)
√Δ=6
| −2−6 | −8 | |||
x1= | = | =−4 | ||
| 2 | 2 |
| −2+6 | 4 | |||
x2= | = | =2 | ||
| 2 | 2 |
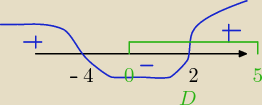 dla −4 ↗↘ czyli max , ale nie załapuje się w dziedzinie
dla 2 ↘↗ czyli min f(2)=23+3*22−24*2+4=−24 −wartosc najmniejsza
f(0)=4
f(5)=84 −wartosc najwieksza
dla −4 ↗↘ czyli max , ale nie załapuje się w dziedzinie
dla 2 ↘↗ czyli min f(2)=23+3*22−24*2+4=−24 −wartosc najmniejsza
f(0)=4
f(5)=84 −wartosc najwieksza