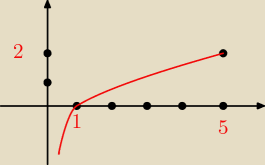
funkcja log Katarina: Na rysunku obok przedstawiono wykres funkcji f(x)=log_ax a) oblicz a b) naszkicuj wykres funkcji g(x)= |f(x+1)−2| i wyznacz dodatnią taką liczbę x dla której spełnione jest równanie g(0)=g(x) a) √5 =a f(x)=log_√5 x b) narysować wyres umiem, ale nie rozumiem dalszej części punktu B dotyczącej równania g(0)=g(x) czy mogłabym liczyć na pomoc?

Katarina: (1;0) i (5;2)).

Katarina: punkty na wykresie

krystek: 2=log_a5

Katarina: tak to zrobiłam bardziej zależy mi na punkcie B

Katarina: .

krystek: g(0)=If(0+1)−2I =If(1)−2I=I0−2I=2

Katarina: Krystek a umiałbyś rozpisać te równanie ? Wiem że starasz się abym ja głową ruszyła ale trochę nie wiem jak się zabrać za to

Katarina: |(log_√5 x+1)−2| = |(log_√5 0+1)−2|

krystek: g(0)=g(x) If(x−1)−2I=2 Ilog_√5(x−1) −2I=2

krystek: ups (x+1)

krystek: log{√5(x+1)−2=2 lub log_√5(x+1)−2=−2 Pamiętaj o dziedzinie (D;x+1>0)

Katarina: |log_√5(x+1)−2| =2 log_√5(x+1)−2=2 i log_√5(x+1)−2=−2 log_√5(x+1)=0 log_√5(x+1)=−4 log_√5(x+1)=log_√5(√5⁰) log_√5(x+1)=log_√5(√5⁻⁴)

	1
x+1=1 x+1=
	25

	24
x=0 liczy się tylko to x= −
	25

Krystek czy robie prawidłowo?

Katarina: czekaj widzę bład :

Katarina: nie patrz na to hehe

Katarina: log_√5(x+1)−2 = −2 log_√5(x+1) = 0 log_√5(x+1) =log_√5(√5⁰) x+1=1 x=0 log_√5(x+1)−2 = 2 log_√5(x+1) = 4 log_√5(x+1) =log_√5(√5⁴) x+1=25 x=24

krystek: Popraw błedy i będzi ok prxenosząc nie zmieniłaś znaków

Katarina: dzięki za pomoc jak mozesz zerknij jeszcze raz

Katarina: dzięki kolego

krystek: i dodać ,że x₁i x₂ ∊D

krystek: Koleżanką jestem.

Katarina: sugerowałam się nickiem ok dziękuję

krystek: Ok . Powodzenia

Katarina: nie dziękuje