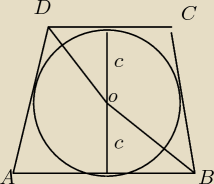
trapez Karlo: jak ktoś masz jeszcze siłe spojrzec, to może choc wskazówkę Dany jest trapez o podstawach a i b opisany na okręgu o promieniu c. Udowodnij, że 4c²≤ab.

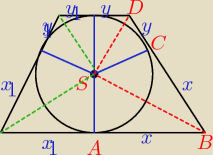
Basia: moim zdaniem jest odwrotnie tr.SAB ~ tr. DCS (to musisz uzasadnić)

c		y
	=
x		c

xy = c² analogicznie x₁y₁ = c² a*b = (x+x₁)(y+y₁) = xy + xy₁+x₁y + x₁y₁ a musi być x₁≤x i y₁≤y (lub na odwrót, ale wtedy dowodzisz tak samo) i są to liczby dodatnie; stąd xy₁≤ xy i x₁y ≤xy czyli ab ≤ xy+xy + xy + x₁y₁ = 4c²

Basia: ale z drugiej strony x₁ ≤ x ⇒ x₁*y₁ ≤ x*y₁ y₁ ≤ y ⇒ x₁*y₁ ≤ x₁*y i mamy a*b ≥ xy + x₁y₁+x₁y₁+x₁y₁ = 4c² stąd wniosek, że a*b = 4c²

Karlo: nie widzę tego podobieństwa

Karlo: juz widze

Karlo: hehe fajnie że je zrobiłem kiedyś

Dominik: . tylko ze trzeba bylo udowodnic, ze jest dokladnie 4c² = ab

Karlo: ale jak spojrzalem na zadanko to prawie odrazu wykrylem to podobieństwo , także dalej już poszło i wykazałem co trzeba