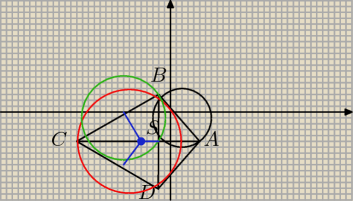
geometria analityczna luzia: Przekątne deltoidu ABCD przecinają się w punkcie S, który znajduje się w III ćwiartce układu współrzędnych. Wyznacz równanie okręgu opisanego na trójkącie BCD, jeżeli okręgi opisane na trójkątach BCS (zielony) i BSA (czarny) mają odpowiednio równania x² + y² + 16x + 12 = 0 i x²+y²−20=0 Wiem że: śr okręgu BCS (−8,0) r=√52 śr okręgu BSA (0,0) r=√20 potem podstawiając 1 równanie okręgu do 2 obliczyłam miejsca przecięcia B=(−2,4) S=(−2,−4) chciałam coś z równań prostych bo równanie szukanego okręgu to miejsce przecięcia się symetralnych trójkąta BCD pr SC y=−4 ale i tak nie wiem co dalej

Basia: napisz równanie pr.BS pr.AC ⊥pr.BS i przechodzi przez S więc napisz jej równanie C to punkt wspólny pr.AC i okręgu BCS BS^→ = SD^→ z tego wyznaczysz D i napiszesz równanie okręgu BCD

luzia: pr BS x=−2 a żeby wyznaczyć C wystarczy podstawić y=−4 do równania okręgu? resztę powinnam dać radę dziękuję bardzo

Basia: tak; wystarczy

luzia: już mam obliczony punkt C =(−14,−4) jeszcze raz dziękuję