Proszę o szybkie zrobienie Piotrek: Oblicz wartosci pozostałych funkcji trygonometrycznych kata; a)tg 2α = 1/3 , 180⁰< α<270⁰ b)sin α= 12/13 ,90⁰<α<180⁰ Udowodnij tożsamość trygonometryczną: a)tg 2 α= 2/ctg α−tgα

klasa1gimnazjum: popunkt A ) 2α=0.3333333 α=0.17 = 9^o zatem konto alfa to 189^o

Basia: nie o to tutaj chodzi

Basia: 2α ∊(180;270) ⇒ α∊(90; 135) ⇒ tgα<0, sinα>0, cosα<0

	2tgα		1
tg2α =		=
	1−tg2α		3

6tgα = 1−tg²α tg²α + 6tgα −1 = 0 Δ = 36+4 = 40 √Δ = √40 = 2√10

	6−2√10
tgα =		= 3−√10
	2

(bo drugi jest >0)

sinα
	= 3−√10
cosα

sinα = (3−√10)cosα sin²α+cos²α=1 (9−6√10+10)cos²α + cos²α = 1 (20−6√10)cos²α = 1

	1		20+6√10		20+6√10
cos2α =		=		=		=
	10−6√10		400 − 36*10		40

10+3√10
20

	10+3√10
cosα = −√
	20

	10+3√10		10+3√10
sinα = (3−√10)*(−√		) = (√10−3)*√
	20		20

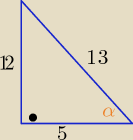Eta: b) α€(90^o, 180^o) to sinα>0 , cosα<0 , tgα<0 , ctgα<0

	12		12		5
cosα= −		, tgα= −		, ctgα= −
	13		5		12

pigor:

	2
..., Udowodnij tożsamość trygonometryczną a) tg 2α=		.
	ctg−tgα

	sin2α		2sinαcosα
L= tg2α=		=		=
	cos2α		cos2α−sin2α

	2sinαcosα		2
=		=		= P . ...
	cosα   sinα   sinαcosα( − )   sinα   cosα		ctgα−tgα

Eta:

	2tgα
L=tg2α=
	1−tg2α

	2		2tgα
P=		=		=P
	1   −tgα tgα		1−tg2α

Eta: By uniknąć pytań ......... wyprowadzam wzór:

	sin2α		2sinαcosα
tg2α=		=		=
	cos2α		cos2α−sin2α

	2sinαcosα   cos2α		2tgα
=		=
	cos2α   sin2α   − cos2α   cos2α		1−tg2α