Prosta y=2x+3 jest symetralną odcinka AB. Oblicz współrzędne punktu A, jeśli B(5 BLS: Prosta y=2x+3 jest symetralną odcinka AB. Oblicz współrzędne punktu A, jeśli B(5,3). Robię to w następujący sposób: y=2x + 3, czyli −2x + y − 3=0. Z tego wynika, że wektor AB=[−2,1]. Jednocześnie wektor AB=[5−m,3−k], gdzie A(m,k). Proces myślowy jest dobry? Bo błędny wynik mi wychodzi, a błędu w obliczeniach nie znajduję. Z góry dzięki za pomoc

Basia: wektor [−2;1] jest prostopadły do symetralnej czyli równoległy do AB^→ ale z tego nie wynika, że jest równy AB^→ napisz równanie pr.AB (jest prostopadła do danej i przechodzi przez B) znajdź ich punkt wspólny D wtedy AD^→ = DB^→

BLS: Jak to nie wynika? Mogłabyś szerzej wyjaśnić dlaczego? Mam mętlik w głowie w tym momencie. Podany sposób rozwiązania rozumiem. Dzięki.

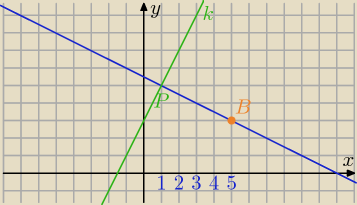
Mila: B(5,3). k: y=2x+3 A jest symetryczny do B względem prostej k. AB⊥k

	−1
y=		x+b i B∊prostej
	2

	−1
3=		*5+b ⇔b=5,5
	2

y=−0,5x+5,5 Teraz szukaj punktu A. Punkt P jest środkiem AB

BLS: Tak jak pisałem, potrafię rozwiązać to zadanie sposobami, które podajecie. Nie bardzo jednak wiem, dlaczego wektor [−2,1] nie jest równy wektorowi AB.

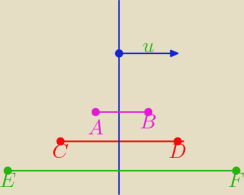
Basia: prosta x=0 jest symetralną każdego odcinka A(x,y) B(−x,y) czy z tego wynika, że wektor [0,0] jest równy wektorowi AB^→ gdzie A(−1,0) B(1,0) ? albo patrz na rysunek niebieska prosta jest symetralną każdego z tych trzech odcinków (a można ich narysować nieskończenie wiele różnych) to czy jeden wektor może być równy i AB^→ i CD^→ i EF^→ ? u^→ jest do każdego z nich równoległy, ale może nie być równy żadnemu (z tych trzech)