Koło
Mokolo: Czy w tym równaniu można znaleźć równanie koła: x2 + (|y| − 2)2 = 16
Wzór na postac kanoniczną koła; (x −a)2 + (y −b)2 = r2
14 kwi 18:50
jikA:
Dla y ≥ 0 otrzymujesz
x2 + (y − 2)2 = 16
dla y < 0 dostajesz
x2 + (y + 2)2 = 16.
14 kwi 18:54
Mokolo: A czy mozna z tego wzoru narysować koło w ukladzie współrzędnych ?
14 kwi 18:56
jikA:
Tak pamiętając że
dla y ≥ 0 masz postać x2 + (y − 2)2 = 16
dla y < 0 masz x2 + (y + 2)2 = 16.
14 kwi 19:00
jikA:
Tylko to nie jest koło to będą kawałki okręgu.
14 kwi 19:03
kylo1303: W drugim przypadku byłoby:
x2 − (y+2)2=16 a to już nie jest równanie okręgu
14 kwi 19:04
Mokolo: dlaczego
14 kwi 19:05
xxx:
Kylo1303 pomyśl dobrze
14 kwi 19:07
jikA:
kylo1303 niestety to co piszesz jest nie prawdą.
x2 + (−y − 2)2 = 16
x2 + [−(y + 2)]2 = 16
x2 + (−1)2 * (y + 2)2 = 16
x2 + 1 * (y + 2)2 = 16
x2 + (y + 2)2 = 16.
14 kwi 19:07
Mokolo: Czyli jak powinien taki okrąg wyglądać w układzie
?
14 kwi 19:14
jikA:
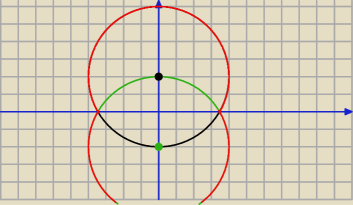
Narysuj sobie najpierw okrąg x2 + (y − 2)2 = 16 i to co jest pod osią OX wymazujesz następnie
rysujesz okrąg x2 + (y + 2)2 = 16 i to co jest nad osią OX wymazujesz.
14 kwi 19:18
Mokolo:
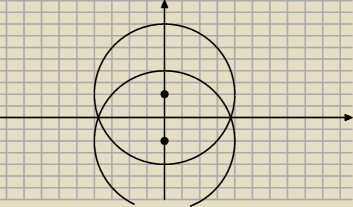
Czyli to będą takie dwa koła o środkach w punktach (0,2) i (0,−2)
14 kwi 19:20
jikA:
Jeszcze raz Ci piszę że to nie są koła tylko okręgi. Napisałem wyżej jak zrobić.
14 kwi 19:22
14 kwi 19:23
14 kwi 19:24
jikA:
Mniej więcej takie coś powinieneś otrzymać.
14 kwi 19:27
Mokolo: ok wielkie dzięki
14 kwi 19:28
jikA:
x2 + (y − 2)2 = 16
x2 + (y + 2)2 = 16
x2 + (|y| − 2)2 = 16.
14 kwi 19:29
Krzysiek: Mokolo. postac kanoniczna kola jest taka (x−a)2+(y−b)2≤r2
14 kwi 19:30
Mokolo: Mnie na ( etapie pierwszej klasy liceum ) nauczono że ma być taki : (x −a)2 + (y −b)2 = r2
14 kwi 19:33
jikA:
Nie nie nauczono tylko Ty za pewne sobie tak to wpoiłeś że równanie
(x − a)2 + (y − b)2 = r2 opisuje koło a nie okrąg.
14 kwi 19:46
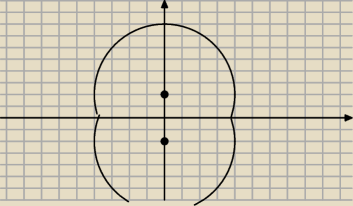Czyli ma być coś takiego