d Aga: Trójkąt równoboczny ABC ma bok długości 10cm. Na jego bokach obrano punkty M,N,P tak, że |AM|=|BN|=|CP|. Jak należy wybrać punkty MNP aby pole trójkąta MNP było najmniejsze? jest to zadania z funkcji kwadratowej i zupelnie nie mam pojęcia jak to zrobic prosze o pomoc

Aga: ponawiam prośbę

Bogdan:

	1
cos60o =
	2

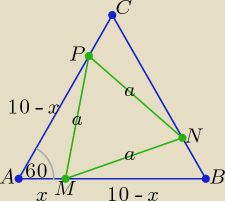
Korzystamy z twierdzenia cosinusów w trójkącie AMP lub MBN lub NCP. a² = x² + (10 − x)² − 2*x*(10 − x)² * cos60^o a² = 3x² − 30x + 100

	√3
Pole trójkąta MNP P =		a2 → min
	4

	√3
P =		(3x2 − 30x + 100)
	4

	3√3		30√3
Otrzymaliśmy funkcję kwadratową P(x) =		x2 −		x + 25√3, która
	4		4

	3√3   10*   4
posiada minimum dla x =		= 5.
	3√3   2*   4

	−b
Przypominam: jeśli f(x) = ax2 + bx + c, to funkcja posiada ekstremum dla x =		.
	2a

Odp. Punkty M, N i P są środkami boków trójkąta ABC.