help! nataszka: help! bardzo bardzo proszę o szybką odp .... w trójkącie prostokątnym o wymiarach 6,8 ,10 z wierzchołka kąta prostego poprowadzono odcinek, którego drugi koniec D należy do przeciwprostokątnej. Oblicz długość odcinka AD jeżeli obwody trójkątów ABD i ADC są równe..

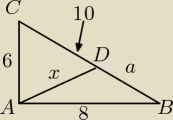
Michal: 6+x+10−a=8+x+a 4=a 6+6+x=8+4+x 12x=12x x=x Zatem x może być dowolną liczbą, ale zauważ, że nie do końca, bo 2 ramiona trójkąta muszą być dłuższe niż trzeci. Zatem 6+6>x; x<12. Zatem x należy do (0,12)

ICSP: źle Michale

ICSP: x = 2,4 √5

Michal: Niby dlaczego źle?

ICSP: ponieważ z tego co widzę masz dwie niewiadome : a oraz x ale równanie jest tylko jedno : 6 + x + 10 −a = 8 + x + a powiedz mi co się stanie gdy rozwiązujesz układ równań z dwoma niewiadomymi mając tylko jedno równanie ?

Michal: jak to, masz 2 równania, przyrównałem je do siebie po prostu. Mogę zapisać, jako układ równań Ob=.. i drugie Ob=... i przyrównam.

ICSP: to pokaż mi prosze te dwa równania. Oczywiście bez wprowadzania trzeciej niewiadomej ( Ob)

Aga1.: Z trójkąta prostokątnego wylicz cosinus kąta i x wylicz z twierdzenia cosinusów.

ICSP: Aga1 Pytanko dodatkowe: Załóżmy żę jestem uczniem który nie zna twierdzenia cos. Czy mogę obliczyć odcinek x za pomocą podstawowych własności ?

Michal: Dam Ci inny przykład. Jaś z kolegą Andrzejem, chodzili codziennie na lody, bo było ciepło. Pierwszego dnia kupili 11 gałek i podzielili się(11−z i z), następnego zjedli tyle samo gałek(x), a jeszcze kolejnego Andrzej zjadł 3 gałki, a Jaś 6. Policz ile zjedli tyle samo gałek. Dla mnie to bez sensu, bo tyle samo, to tyle samo, nie ta liczba jest niewiadomą, tylko kiedy się podzielili, a zauważ, że to x się skraca. x+z+3=x+11−z+6 z+3=11−z+6 2z=14 z=7 Podłóż z=7 x+7+3=x+11−7+6 x+10=x+10 x=x

Michal: Powiedz, gdzie błąd robię, bo rozumiem, że wiesz gdzie robię.

ICSP: ale jeżeli x = 2 to otrzymujemy ze zjedli więcej gałek niż mieli

Michal: x może być 100,200 ale również 2, co za różnica? Powiedziane, jest tylko, że tyle samo zjedli, tzn. jeżeli jaś zjadł 2 to i andrzej musiał też tyle zjeść. Czemu niby stwierdzenie, że zjedli więcej gałek niż mieli? x należy do liczb naturalnych, tylko tyle wiesz z zadania.

ICSP: czyli jest za mało danych w drugim zadaniu aby je rozwiązać. Zawsze będzie wychodziła tożsamość. Gdy masz o jedno równanie mniej od ilości niewiadomych jest duża szansa na to że dostaniesz tożsamość. w twoim przypadku masz jedno równanie : 6 + x + 10 − a = 8 + x + a i teraz operujesz sobie od tak na tym równaniu najpierw skracasz x i wyliczasz a a = 4 i w tym momencie długość odcinka x jest już [C{jednoznacznie]] ustalona. Narysuj sobie trójkąt prostokątny o przyprostokątnych 6 i 8 , przeciwprostokątna 10 i odcinek który dzieli przeciwprostokątną na odcinki 4 oraz 6. Następnie spróbuj narysować drugi odcinek x który podzieli przeciwprostokątną na takie same odcinki i dodatkowo będzie spełniony warunek z obwodami

Michal: no ale, zauważ, że jeżeli jeden bok mają wspólny, to do równości obu obwodów, ten bok nie "wyrównuje" ich długości, ponieważ mają wspólny ten bok. Teraz przypatrzyłem się jeszcze raz i przecież x ,czyli |AD| musi należeć do (2,12), dlaczego? Ponieważ 2 boki muszą być większe(nie równe) od 3−go z czego 2 jest wyłączone. A w twojej odpowiedzi 2 należy, jako odpowiedź. Podaj mi zatem boki obu trójkątów, wliczając, że jeden ma boki 6,2,x(x= odcinkowi |CD|) a drugi ma boki 8,2, y(y= odcinkowi |DB|). Tutaj na tym przykładzie chyba jest to widoczne od razu. Rozwinę i udowodnię to bardziej co napisałem. Jeden bok jest równy 6, drugi 8 tak? Skoro tak jest to musisz do pierwszego boku dodać 2, żeby wyrównać tak? Skąd to bierzesz? Nie z długości |AD| bo są zależne od siebie i jeżeli dodasz do boku |AD| 2 to nie wyrówna ci tej różnicy w bokach 6 i 8, ponieważ, w drugim trójkącie doda się też 2 i koło się zamyka. Zatem jedynie z przeciwprostokątnej możesz to zrobić. Wychodzi na to, że długość odcinka |CD| musi być dłuższa o 2 od odcinka |BD|.

ICSP: oczywiście że musi być dłuższa. Ja nie twierdzę inaczej. U mnie |CD| = 6 a |BD| = 4 Obwody tych trójkątów są równe i jednocześnie ustaliłem pkt D (JEDNOZNACZNIE) czyli jeżeli teraz narysujesz trójkąt to D będziesz zmógł postawić tylko w jednym miejscu tak ? Zatem jego odległość od pkt A również musi być tylko jedna, a nie dowolna jak twierdzisz

Aga1.:

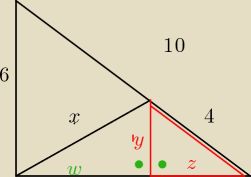
	y		6
Trójkąt czerwony i trójkąt o bokach 6,8,10 są podobne.		=
	4		10

y= Teraz twierdzeniem Pitagorasa. z²=16−y² z= w=8−z x²=w²+y² x= ( szukany odcinek)

Aga1.: Witajcie . ICSP masz jeszcze inny pomysł na rozwiązanie tego zadania?