funkcje Hmm: Wykaż, że funkcja określona wzorem f(x) = (3x² − 4x + 12) / (x² + 4) , gdzie x należy do R, przyjmuje najmniejszą wartość równą 2, zaś największą równą 4.

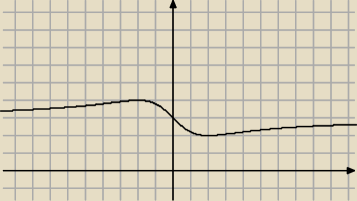
Aga1.: Oto wykres tej funkcji.Znasz pochodne?

Hmm: niestety nie znam

pigor: ..., otóż, np. tak :

	3x2−4x+12
y=		⇔ x2y+4y= 3x2−4x+12 ⇔ (y−3)x2+4x+4y−12 ⇔
	x2+4

⇔ 3−y≠0 i Δ_x= 16−4(y−3)(4y−12) ≥0 /:16 ⇔ y≠3 i 1−(y−3)² ≥0 ⇒ ⇒ (1−y+3)(1+y−3) ≥0 ⇔ (−y+4)(y−2) ≥0 /: (−1) ⇔ (y−4)(y−2) ≤ 0 ⇔ y∊[2;4] c.n.w.

Hmm: a czy da się zrobić to zadanie nie znając wykresu i pochodnych?

Jelen: Sądzę że da się choć wyjaśnienie będzie trudne

	3x2−4x+12		3(x2+4)−4x
f(x) =		=		=
	x2+4		x2+4

	3(x2+4)		4x		4x
		−		= 3 −
	x2+4		x2+4		x2+4

	4x
Zatem f(x) = 3 −		gdzie x ∊ R
	x2+4

Aby wyznaczyć najmniejszą (największą) wartość funkcji, należy określić wartość wyrażenia

4x		4x
	. W tym celu rozważmy funkcję h(x) =		gdzie x∊ R i wyznaczmy jej zbiór
x2+4		x2+4

wartości. Funkcja h jest funkcją nieparzystą ( udowodnij ten fakt !), więc jej wykres jest symetryczny względem punktu (0,0). Jeśli wyznaczymy największą wartość funkcji h, bez trudu wskażemy też jej wartość najmniejszą. Dla dowolniej liczby rzeczywistej prawdziwej jest nie równość: (x−2)² ≥0 ⇒x²−4x+4 ≥0 czyli x²+4≥4x /: (x²+4) stąd

	4x
1≥		⇒ dla dowolnej liczby x∊R
	x2+4

	4x
Zauważ że funkcja h(x) =		przyjmuje największą wartość równą 1, dla argumentu .
	x2+4

Zatem jej najmniejszą wartość jest −1(dla argumentu −2). Zatem

	4x		4x
−1≤		≤1 /*(−1) czyli ⇒ −1≤−		≤ 1 /+3
	x2+4		x2+4

	4x
skąd 2≤3−		≤4
	x2+4

	4x
Wobec tego funkcja f(x) = 3 −		przyjmuje najmniejszą wartość równą 2 ,a największą
	x2+4

równą 4 Co było do wykazania