logarytmy Włóczykij: funkcja logarytmiczna z parametrem Dla jakich wartości parametru m równanie: (log₃x)²−log₃x²=m ma 2 rozwiązania należące do przedziału <1;∞) ? D:x∊R₊ (log₃x)²−2log₃x=m log₃x=k k²−2k−m=0 Δ=4+4m Δ>0 ⇒ 4+4m>0 ⇒ m>−1 szukam wartości parametru, dla których parabola ma 2 miejsca zerowe nalezące do przedziału <1;∞) x_w>1 ⇒ z tego dostaję sprzeczność f(1)≥0 ⇒ m≤−1 Czyli wychodziłoby że nie ma takiego m. Ale coś czuję, że gdzieś jest błąd. Mógłby ktoś rzucić okiem?

Włóczykij: chyba, że przyjmę Δ≥0 wtedy odpowiedzią byłoby m=−1 i jest jeden podwójny pierwiastek. http://www.wolframalpha.com/input/?i=(log3x)^2-log3+x^2%2B1%3D0+from+x%3D0+to+x%3D10 niby w poleceniu nie chcą 'różnych', ale ciężko się to interpretuje.

Włóczykij: podbijam

Włóczykij: i jeszcze raz, może ktoś zauważył błąd?

pigor: ... mnie wychodzi −1 ≤ m ≤ 0 , czyli m∊[−1;0] . ...

Włóczykij: ok, a widzisz gdzieś błąd w moich obliczeniach / sposobie?

Włóczykij: ?

Włóczykij: up

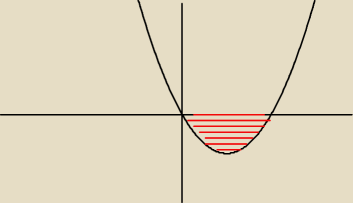
janek: hmm, łatwiej jest chyba po prostu narysowaćparabolkę k²−2k wtedy otrzymujesz, że k=0 lub k=2, skoro k=0 masz log₃x=0 3⁰=x=1, czyli masz początek przedziału, więc ucinamy, od k=0, a dwa rozwiązania ma tam gdzie zakreskowane, czyli wiemy, że m≤0, natomiast dolny przedział znajdziemy tak, że k_w=1 stąd k²−2k=−1=m, czyli mamy dolny przedział, wniosek? m∊<−1;0>