pilne! ewa: na boku AC trójkąta ABC zaznaczono punkty D, E w taki sposób, że |AE| = |ED|= |DC|. przez punkty E, D poprowadzono prostą równoległą do boku AB, które podzieliły trójkąt na trzy rozłączne figury o polach P1, P2 , P3. zatem : A. P2 : P3 = 1 : 2 B.P2 : P3 = 2 : 3 C.P2 : P3 = 4 : 9 D. P2 : P3 = 3 : 5 proszę o obliczenia.

ewa: prosze!

ewa: nikt nie wie?

Mila: Stosunek pół figur podobnych jest równy kwadratowi skali podobieństwa.

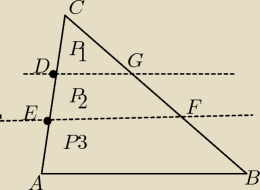
	DC		1
ΔDGC∼ΔABC w skali k=		=
	AC		3

	1
P1=		PΔABC
	9

	EC		2
ΔEFC∼ΔABC w skali k=		=
	AC		3

	4
PΔEFC=		PΔABC
	9

	4		1		3
P2=		PΔABC−		PΔABC=		PΔABC=
	9		9		9

	4		5
P3=PΔABC−PΔEFC=PΔABC−		PΔABC=		PΔABC
	9		9

	3		5		3		5
P2: P3=(		PΔABC):(		PΔABC)=		:		=3:5
	9		9		9		9

Mila: Stosunek pół figur podobnych jest równy kwadratowi skali podobieństwa.

	DC		1
ΔDGC∼ΔABC w skali k=		=
	AC		3

	1
P1=		PΔABC
	9

	EC		2
ΔEFC∼ΔABC w skali k=		=
	AC		3

	4
PΔEFC=		PΔABC
	9

	4		1		3
P2=		PΔABC−		PΔABC=		PΔABC=
	9		9		9

	4		5
P3=PΔABC−PΔEFC=PΔABC−		PΔABC=		PΔABC
	9		9

	3		5		3		5
P2: P3=(		PΔABC):(		PΔABC)=		:		=3:5
	9		9		9		9