Geometria
Pan Adam: Przeglądam sobie właśnie zbiór zadań mojego ojca, stary jak świat i widzę takie zadanko:
Który z równoległoboków wpisany w dany trójkąt równoramienny, w ten sposób, że jeden bok
równoległoboku jest zawarty w podstawie trójkąta, drugi bok w jednym ramieniu trójkąta,
czwarty wierzchołek zaś należy do drugiego ramienia danego trójkąta, ma największe pole?
Nie do końca rozumiem o co tu chodzi. Jak to "który z równoległoboków"?!
12 kwi 20:43
Pan Adam: odp to romb? Nie mam pojęcia a odpowiedzi nie ma. Kwadrata się tu nie wstawi, prostokąta też
nie. Pozostaje romb lub zwykły równoległobok ewentualnie. Jeżeli gadam głupoty to proszę
wybaczyć ale szybko chciałbym się dowiedzieć jak w ogóle się do tego zabrać
12 kwi 20:45
PW: Mogą być "niskie i szerokie" , ale mogą być "wysokie i chude", pole jest zmienne − zależy od
długości boku leżącego na podstawie. Należy wyznaczyć pole równoległoboku jako funkcję
długości podstawy i zbadać gdzie funkcja osiąga maksimum.
12 kwi 20:50
krystek:
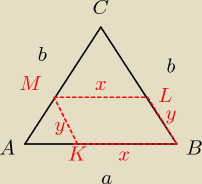
12 kwi 20:53
Mila:
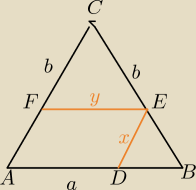
Szukasz x i y w zależności od boków trójkata.
12 kwi 20:55
Pan Adam: Ma może ktoś pomysł jak by to zacząć?
12 kwi 21:12
PW: Te dwa małe odcięte trójkąty są podobne do dużego, jeden ma wysokość u, a drugi h−u, gdzie h
oznacza wysokość dużego trójkąta., może więc zmienną uczynić u? Stosunek pól jest równy
kwadratowi stosunku wysokości (skali podobieństwa).
12 kwi 21:32
Pan Adam: ciekawe... dzięki
12 kwi 22:02
Mila: ΔCFE∼ΔABC⇔
∡CAB=α
h− wysokość opuszczona na AB.
| b−x | | b | | (b−x)*a | |
| = |
| ⇔(b−x)*a=y*b⇔y= |
| |
| y | | a | | b | |
| | (b−x)*a | | √b2−o,25a2 | |
P▱(x)=x*y*sinα=x* |
| * |
| |
| | b | | b | |
| | a√b2−0,25a2 | | a√b2−0,25a2 | |
P▱(x)=x*(b−x)* |
| , |
| >0 stała |
| | b2 | | b2 | |
P
▱(x) ma największą wartość w wierzchołku paraboli
12 kwi 22:47

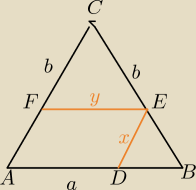 Szukasz x i y w zależności od boków trójkata.
Szukasz x i y w zależności od boków trójkata.