Arkusz XXV Testy maturalne wyd. Aksjomat
matura: 
Uprzejmie proszę o pomoc.
Czemu funkcja −2x kwadrat jest malejąca w przedziale (0, ∞)?
12 kwi 20:03
ICSP: bo jest smutna

12 kwi 20:06
Nienor: Bo im większe x wstawiasz, tym mniejsze otrzymujesz y.
12 kwi 20:15
PW: Na rysunku widać od razu: im dalej z dodatnimi x, tym wykres leży niżej.Formalny dowód polega
na wzięciu dowolnych dwóch x1 i x2 z przedziału (0,∞) i pokazaniu, że jeżeli x1<x2, to
−x12>−x22 − zgodnie z definicją funkcji malejącej.
Dowód. Jeżeli x1<x2, to po pomnożeniu stronami przez (−x1) otrzymamy
(1) −x12>−x1x2
Zmieniliśmy nierówność na przeciwną, gdyż mnożyliśmy przez liczbą ujemną.
Pomnożenie nierówności
x1<x2
przez (−x2) daje
(2) −x1x2>−x22.
Z (1) i (2) wynika, że
−x12>−x22,
co kończy dowód
12 kwi 20:16
PW: Ja tu dłubię na poważnie, a tymczasem już napłynęły dwie odpowiedzi, bardziej mi sie podoba
ICSP.
12 kwi 20:18
matura: ahaaaa

czyli w miejscu x = 0 linie paraboli idą w dół czyli robi się smutna

A czemu
rozwiązaniem nierówności xlog0,5 liczby 3 <log0,5 liczby 3 jest zbiór (1,∞) ?
12 kwi 20:26
PW: (x−1)log0,53<0
Drugi czynnik jest ujemny, a pierwszy dodatni dla x>1, tak więc iloczyn jest ujemny dla x>1.
12 kwi 20:32
matura: ja to pierwsze rozumiem tak: −2xkwadrat=0x=0, a =−1, zaznaczam x= 0 na osi, linie paraboli ida
w dół, malejąca funkcja jest od 0 do ∞. Good?
12 kwi 20:34
mika:
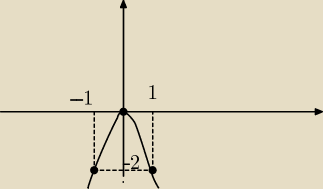
a=−2
12 kwi 20:37
PW: No tak, ale to jest obrazek, ilustracja. Poważny dowód na pytanie "udowodnij, że f(x)=−x2 jest
malejąca na przedziale (0,∞)" podałem, i nie da się tego zrobić przyjemniej, można ewentualnie
badać różnicę
−x12−(−x22) = (x2−x1)(x2+x1)
i pokazać, że jest dodatnia, to chyba przebiega szybciej i jest bardziej zrozumiałe.
Dla siebie − obrazek, funkcja opada, jest smutna. Jako dowód − tylko stosowny rachunek. Wykres
funkcji nie może być dowodem, to powstał w odwrotnej kolejności − najpierw ktoś zbadał, że
funkcja jest rosnąca, a potem narysował wykres.
12 kwi 20:45
matura: Może mi ktoś dokładniej wytłumaczyć z tymi logarytmami ?
12 kwi 21:07
PW: 3<1
log0,53>log0,51
log0,53>0
Funkcja log0,5 jest malejąca, więc przy przejściu od pierwszego wiersza do drugiego
zmieniliśmy nierówność na przeciwną
12 kwi 21:15
PW: No ładnie, napisałem przeciwne nierówności niż być powinny, jestem chyba pierwszy, co twierdzi,
że 3<1. Pozamieniaj, będzie dobrze: log0,5<0, tak jak to pisałem o 20:32 (jakoś w pamięci
rozwiązałem bez błędu).
12 kwi 21:19
 Uprzejmie proszę o pomoc.
Czemu funkcja −2x kwadrat jest malejąca w przedziale (0, ∞)?
Uprzejmie proszę o pomoc.
Czemu funkcja −2x kwadrat jest malejąca w przedziale (0, ∞)?

 czyli w miejscu x = 0 linie paraboli idą w dół czyli robi się smutna
czyli w miejscu x = 0 linie paraboli idą w dół czyli robi się smutna A czemu
rozwiązaniem nierówności xlog0,5 liczby 3 <log0,5 liczby 3 jest zbiór (1,∞) ?
A czemu
rozwiązaniem nierówności xlog0,5 liczby 3 <log0,5 liczby 3 jest zbiór (1,∞) ?
 a=−2
a=−2