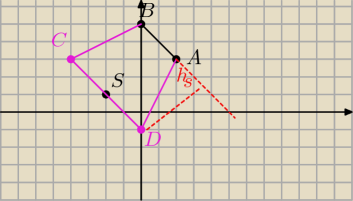
Odcinek o końcach A (2, 3) i B (0, 5) jest podstawą trapezu ABCD. Druga podstawa, o środku w
punkcie S (−2, 1), jest dwa razy dłuższa od podstawy AB. Wyznacz współrzędne wierzchołków C i
D. Oblicz objętość bryły powstałej przez obrót trapezu ABCD wokół prostej AB.
AB→=[−2,2]
S=(−2,1)→translacja [−2,2]→C=(−2+(−2),1+2)=(−4,3)
S=(−2,1)→translacja [2,−2]→D=(0,−1)
CD: y=−x−1
x+y+1=0
odległość B=(0,5) od prostej CD
| |5+1| | 6 | |||
h= | = | =3√2 | ||
| 12+12 | √2 |
| 1 | ||
Vbryły=π*(3√2)2*4√2−2* | π*(3√2)2*√2=60π√2 | |
| 3 |
