Iloczyn sinusów z ich sumy TAK: Suma sinusów kątów ostrych w pewnym trójkącie prostokątnym jest równa 3√5/5. Oblicz: −iloczyn sinusów tych kątów −iloczyn cosinusów tych kątów

PW:

	a		b
Podnieś sumę sinusów do kwadratu (zapisując sinusy "z definicji" − jako		i		)
	c		c

i skorzystaj z twierdzenia Pitagorasa.

TAK: Nadal nie rozumiem

TAK:

a2+b2		9
	=
c2		5

a²+b²=9 i c²=5 , czyli a+b=3 i c=√5

a		b
	*		=
√5		√5

Dobrze robię? Jeśli tak to co dalej?

PW: Suma sinusów podniesiona do kwadratu to

	a		b		a2+2ab+b2
(		+		)2 =
	c		c		c2

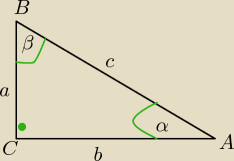
Mila: α,β,− kąty ostre

	a
sinα=		=cosβ
	c

	b
sinβ=		=cosα
	c

	3√5
sinα+sinβ=		2
	5

	9
sin2α+2sinα*sinβ+sin2β=		⇔
	5

	9
sin2α+2sinα*sinβ+cos2α=
	5

	4
2sinα*sinβ=
	5

	2
sinα*sinβ=
	5

cosα*cosβ=?

	2
cosα*cosβ=sinβ*sinα=
	5

Mila: ?