giągi Kamila: Proszę o pomoc: Oblicz sumę stu najmniejszych dodatnich rozwiązań równania sin2x=cosx obliczyłam pierwiastki cosx=0 i sinx=¹₂ pierwsze początkowe mam π/6 π/2 π5/6 nir eirm jak to dalej robić może mi ktoś wytłumaczyć? wiem że trzeba ciągi

***: Dokładnie to chyba 2475π−w mierze łukowej ***−łebmajster,artur miast z matematyki to z telewizji,oraz szlaban(***bo się nie mieści)

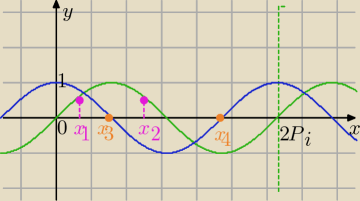
Mila: Rozważam rozwiązania w przedziale <0,2π> 1) y=sin(x)

	1
sinx=
	2

	π		5π
x1=		lub x2=
	6		6

2)y=cosx cosx=0

	π		3π
x3=		lub x4=
	2		2

3) okresem obu funkcji jest T=2π Rozwiązania ( każde osobno) tworzą ciągi arytmetyczne r=2π

	π
a) a1=x1=
	6

	π
an=		+(n−1)*2π
	6

obliczamy sumę 25 wyrazów tego ciągu

	π   π   + +24*2π 6   6		1
Sa25=		*25 =604		π
	2		6

	π
b) b1=x2=
	2

	π		π
bn=		+(n−1)*2π, b25=		+24*2π
	2		2

	π   π   + +24*2π 2   2		1
S25b=		*25=612		π
	2		2

	5π
c) c1=
	6

	5π		5π
cn=		+(n−1)*2π, c25=		+24*2π
	6		6

	5π   5π   + +24*2π 6   6		5
S25c=		*25=620		π
	2		6

	3
d) d1=		π
	2

	3		3
dn=		π+(n−1)*2π, d25=		π+24*2π
	2		2

	3   3   π+ π+24*2π 2   2		1
S25d=		*25=637		π
	2		2

	1		1		5		1
604		π+612		π+620		π+637		π=2475π
	6		2		6		2

Mila: Oj, widzę, że nie warto było się trudzić. Kamila nie czyta.