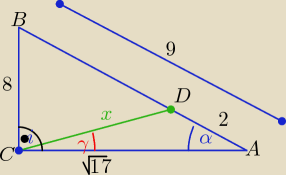
Trójkąt prostokątny Bardzo proszę o pomoc: Zadanie 5 (6 pkt.) W trójkącie prostokątnym ABC przyprostokątne mają długości |BC| = 8, |CA| = √17. Na boku AB wybrano punkt D tak, że |AD| = 2 . Oblicz sinus kąta DCA . Rysunek: http://img.zadania.info/zes/2/0076892/HzesR55x.gif Część rozwiązania: Stosując twierdzenie sinusów w trójkątach ADC i BCD mamy http://img.zadania.info/zes/2/0076892/HzesR60x.gif Bardzo proszę o pomoc w szczególności z tą drugą linijką. Wg. mojego myślenia Cos β = |CD| do |AC| zaś sin 90 stopni − α, to |BD| do |BC| więc skąd ta druga zależność

Bardzo proszę o pomoc: wie ktoś jak to zrobić? błagam o pomoc.

Eta:

	√17		8
|AB|= 9 cosα=		i sinα=
	9		9

z tw. cosinusów w ΔDCA

	121
x2= 22+(√17)2−2*2*√17*cosα=............ =
	9

	11
x=
	3

teraz ze wzoru sinusów w ΔDCA:

2		x		16
	=		⇒ sinγ= ........... =
sinγ		sinα		33

i to wszystko