 a = tg α = √3 α = 60o
y = a x + b = √3 x + b oraz A = ( − 2 ; 3)
Prosta ma przechodzić przez punkt A , więc
3 = √3*( −2) + b ⇒ b = 3 + 2√3
Równanie prostej
y = √3 x + 3 + 2√3
==================
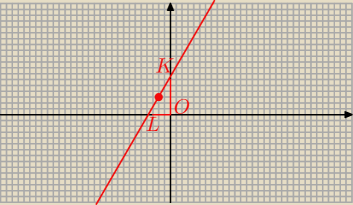
Dla x = 0 jest y = 3 + 2√3 więc K = ( 0; 3 + 2p{3] )
Dla y = 0 jest 0 = √3 x + 3 + 2√3 ⇔ √3 x = − 3 − 2√3 ⇔ x = − √3 − 2
więc L = ( − 2 − √3 ; 0 )
O = ( 0 ; 0)
ΔKLO jest prostokątny, więc jego pole
P = 0,5 *I LO I * I KO I = 0,5* ( 0 − ( − 2 − √3))*( 3 + 2 √3 − 0 ) =
= 0,5*( 2 + √3)*( 3 +2√3) = 0,5*( 6 + 4√3 + 3√3 + 6) = 0,5*( 12 + 7√3) =
= 6 + 3,5 √3 ≈ 12
===========
a = tg α = √3 α = 60o
y = a x + b = √3 x + b oraz A = ( − 2 ; 3)
Prosta ma przechodzić przez punkt A , więc
3 = √3*( −2) + b ⇒ b = 3 + 2√3
Równanie prostej
y = √3 x + 3 + 2√3
==================
Dla x = 0 jest y = 3 + 2√3 więc K = ( 0; 3 + 2p{3] )
Dla y = 0 jest 0 = √3 x + 3 + 2√3 ⇔ √3 x = − 3 − 2√3 ⇔ x = − √3 − 2
więc L = ( − 2 − √3 ; 0 )
O = ( 0 ; 0)
ΔKLO jest prostokątny, więc jego pole
P = 0,5 *I LO I * I KO I = 0,5* ( 0 − ( − 2 − √3))*( 3 + 2 √3 − 0 ) =
= 0,5*( 2 + √3)*( 3 +2√3) = 0,5*( 6 + 4√3 + 3√3 + 6) = 0,5*( 12 + 7√3) =
= 6 + 3,5 √3 ≈ 12
===========
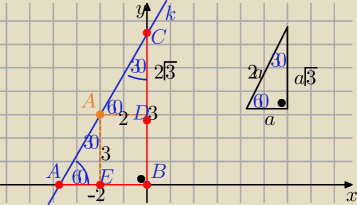 k: y=ax+b , a=tgα ⇒α=60o mamy trójkąty prostokątne o kątach : 30o,60o, 90o
|AE|=√3 , |DC|=2√3
to: |AB|=2+√3, |BC|=3+2√3
k: y=ax+b , a=tgα ⇒α=60o mamy trójkąty prostokątne o kątach : 30o,60o, 90o
|AE|=√3 , |DC|=2√3
to: |AB|=2+√3, |BC|=3+2√3
| 1 | 1 | |||
P(ABC)= | (2+√3)(3+2√3)= | *(12+7√3)= 6+3,5√3 | ||
| 2 | 2 |