planimetria Aleksander: Dany jest trapez, do którego narysowano przekątne, gdzie P1 = 90 , a P2=15 jak na rysunku (zacieniowane trójkątty). Oblicz pole całego trapezu. http://imgur.com/52ej1OE

Aleksander: Wie ktoś może?

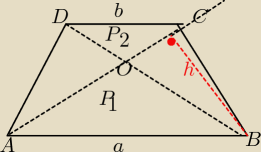
Mila: P₁=90 P₂=15

	a
ΔABO∼ΔDCO w skali k=
	b

Stosunek pól figur podobnych jest równy kwadratowi skali podobieństwa, zatem

P1		90		30		6
	=		=		=		=k2
P2		15		5		1

a		√6
	=
b		1

z podobieństwa ΔABO i ΔDCO ⇒

AO		√6		|AO|
	=		⇔|AO|=√6|OC|⇔|OC|=
OC		1		√6

ΔCOB ma tę samą wysokość , co ΔBOC

	1		90		90√6
PΔCOB=		*90=		=		=15√6=PΔDOC
	√6		√6		6