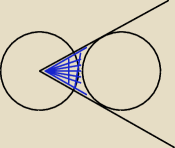
 Dwa okręgi o równych promieniach są styczne zewnętrznie. Ze środka jednego z nich poprowadzono
styczne do drugiego okręgu (rysunek). Wykaż, że pole koła ograniczonego każdym z tych okręgów
jest równe 3Pπ3√3−π, gdzie P jest polem zacieniowanej figury.
(tam π jest pod ułamkiem nie za ułamkiem)
Dwa okręgi o równych promieniach są styczne zewnętrznie. Ze środka jednego z nich poprowadzono
styczne do drugiego okręgu (rysunek). Wykaż, że pole koła ograniczonego każdym z tych okręgów
jest równe 3Pπ3√3−π, gdzie P jest polem zacieniowanej figury.
(tam π jest pod ułamkiem nie za ułamkiem)
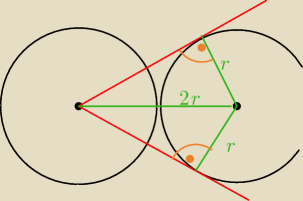 Pole koła ograniczonego każdym z tych okręgów
Pole koła ograniczonego każdym z tych okręgów  Wniosek 1)
Oba okręgi mają takie same promienia (r)
Wniosek 1)
Oba okręgi mają takie same promienia (r)