Sprawdź, które wyrazy ciągu (a_n) są oddalone, jeżeli... wajdzik:

	1
Sprawdź, które wyrazy ciągu (an) są oddalone od 2 o mniej niż		, jeżeli:
	100

	n		2		3		4		5		6
a) an=		1;		;		;		;		;		;...
	2n−1		3		5		7		9		11

Im większe n,tym wyraz a_n jest coraz bardziej oddalony od liczby 2. Będą to "prawie wszystkie wyrazy ciągu?" Proszę o pomoc

pigor: ... rozwiąż sobie w zbiorze n∊N nierówność |a_n−2|<0,01 ⇔ |ⁿ_2n−1−2|<0,01 ⇔ ... itd. . ...

aniabb: definicja granicy |a_n − 2|<0,01

	n
|		− 2|<0,01
	2n−1

	n
−0,01 <		− 2 < 0,01 /+2
	2n−1

	n
1,99 <		< 2,1
	2n−1

	n		n
1,99 <		i		<2,01
	2n−1		2n−1

itd wyliczasz n możesz mnozyć przez mianownik bezkarnie bo na pewno dodatni

pigor: ..., ale wyczułem i w odpowiednim miejscu przerwałem, ...

aniabb: pigor

wajdzik: Wszystko ok, rozumiem. Ale teraz mam pewien problem ... Mianowicie:

n
	<2,01
2n−1

n>2,01(2n−1) n>4,02n−2,01 2,01>4,02n−n 2,01>n(4,02−1) n<0,7 Chyba coś dobrze mi nie wyszło

pigor: ... , dziękuję − na wiosnę jak znalazł − a przerwałem, bo zauważyłem ostatnio na forum wysokie ambicje autora tematu (postu) . ...

pigor: ...hmm, a dlaczego zmieniłeś zwrot znaku nierówności

wajdzik: "Wysokie ambicje" mówisz. Coś w tym jest, ale powiem inaczej. Matematyka to moje życie i lubię liczyć, inna sprawa, że nie zawsze wychodzi ale wierzę, że z czasem to ja będę mógł pomagać innym. Wracając do zadania. Jeszcze raz:

n
	<2,01 /*(2n−1)
2n−1

n<2,01(2n−1) n<4,02n−2,01 2,01<4,02n−n 2,01<n(4,02−1) n>0,7 Przedtem źle przepisałem na początku i policzyłem z błędem.

aniabb: zrób tę drugą część bo wyniki w module są ujemne

wajdzik:

	n
1,99<		/*(2n−1)
	2n−1

1,99(2n−1)<n 3,98−1,99<n 3,98n−n<1,99 1,99>n(3,98−1) n<0,7 Gotowe!

wajdzik: Wszystko się zgadza?

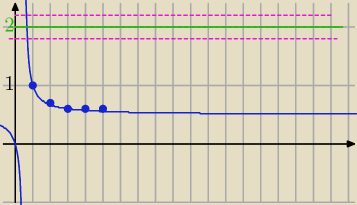
aniabb: tak ..jak widać żadne n nie jest bliżej 2 niż 0,01 bo n∊N

aniabb: więc n<0.07 to zbiór pusty

wajdzik: Ok, dzięki wielkie Aniu.