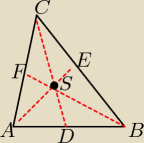
trójkąt Pinka: Dane są wierzchołki A(−1,4) i C(6,−1) trojkata ABC. Oblicz pole tego trojkata, jesli jego środkowe przecinają się w punkcie S(1,−2).

piotrek: znajdz wspolrzedne punktu F, a nastepnie wykorzystaj fakt, ze srodkowe dzielą się w stosunku 2:1. |SB| =2|FS|

Pinka: a jak obliczyc punkt F?

tim: Jak wiemy, środkowa dzieli bok AC na pół.

piotrek: xf = (xa + xc)/2 yf = (ya + yc)/2

Paulaaa: mogę prosi o jakis zarys rozwiazania?

Pinka: a wysokosc to bedzie FB?

piotrek: FB to srodkowa. Wysokość jest zawsze prostopadła do prostej zawierającej podstawę.

Pinka: a wiec jak to zrobic?

piotrek: No dobra. Najlatwiej zrobic to tak. Punkt przeciecia srodkowych to po prostu srodek ciezkosci trojkata. xs = (xa +xb +xc):3 ys = (ya +yb +yc):3 nie masz tylko xb i yb. Majac 3 punkty mozesz wyliczyc pole trojkata.

Pinka: a jak obliczyc pkt B?

Pinka : hmm.. mam te wszystkie punkty (A,B,C), ale skąd wziąć wysokość? proszę o pomoc, tak niewiele brakuje

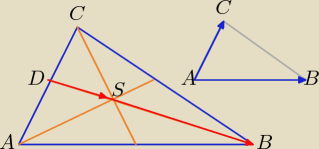
Bogdan: A = (−1, 4), B = (x_B, y_B), C = (6, −1), S = (1, −2)

	−1 + 6		4 − 1		5		3
D = (		,		) = (		,		)
	2		2		2		2

	5		3		3		7
Wektor DS = [1 −		, −2 −		} = [−		, −		], pomijam znak → nad nazwą
	2		2		2		2

wektora,

	3		7
Wektor SB = 2DS ⇒ [xB − 1, yB + 2] = 2[−		, −		]
	2		2

x_B − 1 = −3, y_B + 2 = −7 X_B = −2, y_B = −9 B = (−2, −9) Obliczamy pole trójkąta: Wektor AB = [−2 + 1, −9 − 4] = [−1, −13] Wektor AC = [6 + 1, −1 − 4] = [7, −5] | −1 −13 | Pole trójkąta P = (1/2) * | | | | = (1/2) * |5 + 91| = 48 |7 −5 |

	1
Tu jest		wartości bezwzględnej z wyznacznika drugiego stopnia.
	2

Odp.: Pole trójkąta jest równe 48 j²

piotrek: mialas 3 wspolrzedne x−owe, wiec myslalem, ze znalezc tą ostatnią to nie problem dla Ciebie..