Geometria płaska - trapezoidy paciam27: Oblicz długość przekątnych AC i BD czworokąta ABCD, wykorzystując dane z rysunku poniżej: Link do rysunku: http://pl.static.z-dn.net/files/dce/1d7c8db2bf224e1b19066d9731cd3cf1.jpg Bardzo Was proszę o pomoc

sony: jak zrobić b i c?

sony: proszę o pomoc

nata: b) robimy tak: z Δ ACE obliczamy długość AC = √320= 8√5 z Δ ABE obliczamy AB = 10 Δ ABC jest równoramienny AB=BC=10 oznaczmy punkt przecięcia przekątnych jako P z rysunku AP=PC, więc BD jest symetralną AC, zatem Δ ACD jest równoramienny, wysokość Δ ACD dzieli go na 2 Δ prostokątne, równoramienne, gdzie PD=PC=4√5 z Δ BCP obliczamy BP= 2√5 BD=BP+PD=2√5 + 4√5 = 6√5 c) punkt przecięcia przekątnych oznaczam jako P Δ APD ma kąty: 90, 60, 30⁰, więc AP=2*DP=DB i dalej nie wiem jak udowodnić, że Δ APD jest podobny do Δ BCD − jak to udowodnimy to reszta obliczeń to pikuś − może ktoś pomoże

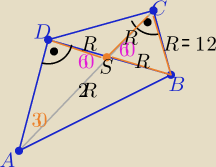
Eta: |DS|=|SB|=|SC|=|BC|=R Trójkąt CBS jest równoboczny o boku długości R=12 W trójkącie ADS o kątach 90^o, 60^o, 30^o |DS|=R to |AS|=2R |AC|=3R=36 , |DB|=2R=24

nata: Eta skąd wiadomo, że ΔBCS jest równoboczny, przecież znamy tylko 1 jego kąt i przeciwległe ramię

nata: ok, już chyba wiem na każdym Δ prostokątnym możemy opisać okrąg, stąd SB=SC i kąt między nimi = 60⁰ (wierzchołkowy), to 2 pozostałe kąty są takie same, czyli też mają po 60⁰ dzięki, a ja tyle nad tym siedziałam

Eta: Dorzucam jeszcze ....