geometria analityczna Tomek: W trójkącie ABC dane są: wierzchołek A(1,0) równanie boku BC: x+3y−13=0 oraz wektor wysokości CD=[2,−2]. Oblicz pole trójkąta ABC.

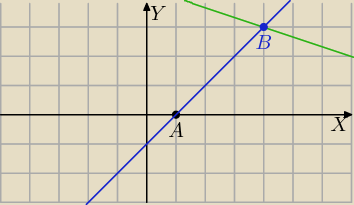
Mila: A(1,0)

	−1		13
równanie boku BC: x+3y−13=0 ⇔3y=−x+13⇔y=		x+
	3		3

oraz wektor wysokości CD=[2,−2]. Oblicz pole trójkąta ABC. CD^→⊥AB Jeśli masz podany wektor prostopadły do prostej, to równanie piszesz tak: AB: Ax+By+C=0 2x−2y+C=0 i A∊prostej AB⇔2*1−2*0+C=0⇔C=−2 AB: 2x−2y−2=0⇔x−y−1=0 y=x−1 Współrzędne B

	−1		13
x−1=		x+
	3		3

x=4 i y=3 B=(4,3) |AB|=√3²+3²=3√2 |CD|=√2²+(−2)²=2√2

	1		1
PΔ=		*|AB|*|CD|=		*3√2*2√2=3
	2		2

P_Δ=3j²