zadanie Kasia: Dane są punkty A=(−1,0), B=(7,2). Na prostej o równaniu y−3 wyznacz taki punkt C, dla którego trójkąt ABC ma najmniejszy obwód. Wykonaj rysunek pomocniczy.

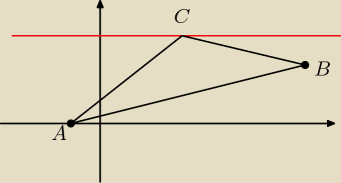
krystek: jeżeli y=3

krystek: Zainteresowany odezwie się zapewne, jak bedzie miał wyliczone. Pozdrawiam forumowiczów.

Krzysiek: Krystek. My Ciebie tez pozdrawiamy

pigor: ..., a więc np. tak: szukasz punktu C=(x,3)=? takiego, że suma odległości s(x)=|AC|+BC|= √x+1)²+3² + √(x−7)²+1² osiąga wartość najmniejszą, a więc ⇔ ⇔ (x=−1 ⇒ s(−1)= 3+√65) lub (x=7 ⇒ s(7)= 1+√73) ⇔ ⇔ (x=−1 ⇒ s(−1) ≈ 11,06) lub (x=7 ⇒ s(7) ≈ 9,54), stąd x=7, czyli punkt C=(7,3) − szukany wierzchołek Δ ABC spełniający warunki zadania . ...

Kasia: Dziękuję za odpowiedź.

ICSP: a to ja może i coś od siebie dorzucę : Otóz szukamy punktu C(x_c ; 3) którego suma odległości od punktu B oraz od pkt A jest najmniejsza gdy : A(−1 ; 0) oraz B(7 ; 2) . tworzę zatem punkt A' który będzie odbiciem pkt A względem prostej y = 3 A'(−1 ; 6) Szukam równania proste A'B

	1
y = −		x + 5,5
	2

oraz sprawdzam dla jakiego x przetnie ona prosta y = 3

	1
3 = −		x + 5,5
	2

1
	x = 2,5
2

x = 5 Odp (5 ; 3)

pigor: .... , o pięknie, masz ICSP rację, a ja nie przyłożyłem się − przyznaję − do tego (czułem to), a to jest właśnie problem najkrótszej drogi do np. "miejsca wybudowania mostu na rzece y=3", tu punktu C=(x,3) , aby wszystkich pogodzić ...

Kasia: To jeszcze raz dziękuję

Kasia: To jeszcze raz dziękuję