Funkcja kwadratowa i trygonometria Matti: Witam, zad 1 Funkcja kwadratowa przjmuje wartości ujemne dla x ∊ (−∞;−2) suma (5;∞), a zbiór wartości tej funkcji to przedział (−∞;4>. Wyznacz wzór funkcji. A więc mamy tak (z racji miejsc zerowych: f(−2)=0 f(5)=0 A z racji wierzchołka f(0)=4 Trzy równania dla funkcji postaci y=ax²+bx+c 4a−2b+c=0 => 4a−2b+4=0 => b=2a+2 25a+5b+c=0 c=4 idąc dalej i podstawiając b z pierwszego równania do drugiego 25a+5(2a+2)+4=0 25a+10a+10+4=0 35a=−14 a=−2/5 b=6/5 Zatem funkcja ma postać y=−2/5x² +6/5x+4. Ktoś potwierdzi moje rozumowanie? Zad 2 Wykaż, że jeśli x i y są kątami ostrymi trójkąta prostokątnego oraz sinx+siny=√5/2 to cosx * cosy= 1/8 tutaj brak pomysłu...

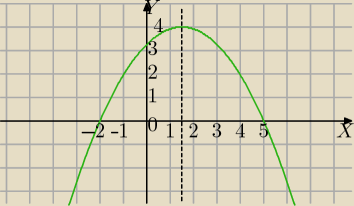
Mila: 1) f(−2)=0 f(5)=0

	−2+5		3
xw=		=
	2		2

	3
f(		)=4
	2

f(x)=a(x+2)(x−5) postać iloczynowa funkcji kwadratowej a<0

	3		3
a(		+2)*(		−5)=4
	2		2

	7		−7
a*		*		=4
	2		2

a*(−49}{4}=4 /*4 −49a=16

	−16
a=
	49

	−16
f(x)=		(x+2)(x−5) postać iloczynowa
	49

Wymnóż, to otrzymasz postać ogólną II sposób

	3
f(x)=a(x−		)2+4 postać kanoniczna
	2

f(−2)=0

	3
a(−2−		)2+4
	2

	49
a*		+4=0
	4

	49
a*		=−4
	4

	16
a=−
	49

	16		3
f(x)=−		(x−		)2+4
	49		2

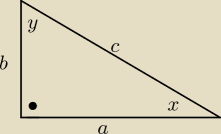
Mila: 2) x,y − kąty ostre i x+y=90, ⇔sinx>0 i siny>0 I sposób− rysunek

	b
sinx=
	c

	a
siny=
	c

	a
cosx=		=siny
	c

	b		√5
cosy=		=sinx⇔równanie sinx+siny=		możemy zastąpić równaniem
	c		2

	√5
sinx+cosx=		/2
	2

	5
sin2x+2sinxcosx+cos2x=
	4

	1
2sinxcosx=
	4

	1		1
sinx*cosx=		⇔cosx*cosy=
	8		8