ostrokątny trójkąt równoramienny patrycja: ostrokątny trójkąt równoramienny ABC o podstawie AB jest wpisany w okręg o środku S, przyczym kąd SAB ma miarę 40℃. oblicz miarę kąta CAB

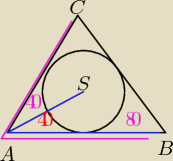
aniabb: CAB ma 80° bo S leży na dwusiecznej

pigor: ... z warunków zadania i własności miar kąta środkowego i wpisanego opartych na tym samym łuku : |∡ACB|=¹₂*40^o= 20^o , zatem z własności kątów Δ i kątów Δ równoramiennego : 2|∡CAB|=180^o−20^o= 160^o /:2 ⇒ |∡CAB|= 80^o . ...

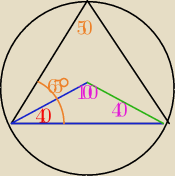
aniabb: Fakt to trójkąt jest WPISANY zatem SBA też 40 więc ASB 100° to ACB 50° 180−50 = 130° 130/2 = 65° szukany kąt CAB

pigor: ...no tak, a ja odczytałem, że dany jest o ASB , przepraszam

patrycja: dzięki