Trójkąty liceum! Ninde: 1. W prostokącie ABCD punkt E jest środkiem boku AB. Przekątna AC i odcinek DE przecinają się w punkcie S. Wykaż, że pole czworokąta EBSC stanowi 5/12 pola prostokąta ABCD. 2. W trójkącie prostokątnym ABC, w którym kąt C=90*, poprowadzono odcinek CD w taki sposób, że D należy do AB oraz kąt BCD= 2 ACD. Wykaż, że jeżeli pola trójkątów ADC i BCD są równe, to kąty ostre trójkąta ABC mają miarę 30* i 60*.

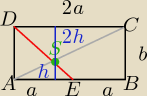
ndawni: ΔASE~ΔDCS z cechy kk

a		h
	=
2a		2h

	1
b=3h⇒h=		b
	3

	2ab		1   a* b   3		5
P EBCS=		−		=		ab
	2		2		6

P EBCS		5   ab 6		5
	=		=
P ABCD		2ab		12

pigor: 2. W trójkącie prostokątnym ABC, w którym kąt C=90^o, poprowadzono odcinek CD w taki sposób, że D należy do AB oraz kąt BCD= 2 ACD. Wykaż, że jeżeli pola trójkątów ADC i BCD są równe, to kąty ostre trójkąta ABC mają miarę 30^o i 60^o. −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− ... , np. tak : niech dla skrócenia zapisu |∡ACD|=γ, |BC|=a, |AC|=b i |∡CBD|= x=? − szukany kąt, to z warunków zadania : P_ΔACD= P_ΔBCD ⇔ ¹₂b*|CD|sinγ= ¹₂a*|CD|sin2y i γ+2γ=90^o ⇒ ⇒ bsinγ= asin2γ i y=30^o ⇒ bsin30^o= asin60^o ⇔ ¹₂b= ¹₂√3a ⇔ ⇔ ^b_a= √3 ⇔ tgx=√3 ⇒ x=60² i |∡CAD|= 90^o−x= 30^o c.n.w.