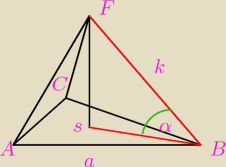
zadanie z ostrosłupem Marta 22: Krawędź boczna ostrosłupa prawidłowego trójkątnego o długości k jest nachylona do podstawy pod kątem α . Wiedząc, że , cosα=0,75 oblicz pole powierzchni całkowitej tego ostrosłupa. mamy trójkąt FSB

	2		a√3
k2 =		*		+
	3		2

	3
cosa =
	4

3		a√3   2
	=
4		k

	4a√3
k=
	9

	a2√3
pole podstawy =
	4

wysokość ściany bocznej:

	1		4a√3
(		a)2 + H2 = (		)2
	2		9

czy pomoze mi ktoś to obliczyć ? wynik mój całkowicie rózni się od właściwego wyniku ( licze na waszą pomoc Drodzy forumowicze

Marta 22: Krawędź boczna ostrosłupa prawidłowego trójkątnego o długości k jest nachylona do podstawy pod kątem α . Wiedząc, że , cosα=0,75 oblicz pole powierzchni całkowitej tego ostrosłupa. mamy trójkąt FSB

	2		a√3
podstawa tego trójkąta =		*
	3		2

	3
cosa =
	4

3		a√3   3
	=
4		k

	4a√3
k=
	9

	a2√3
pole podstawy =
	4

wysokość ściany bocznej:

	1		4a√3
(		a)2 + H2 = (		)2
	2		9

POPRAWKA BO kilka błedów zobaczyłam

Basia:

	a√3
hp =
	2

	2		2		a√3		a√3
x =		*hp =		*		=
	3		3		2		3

	x
cosα =
	k

	3
x = k*cosα =		k
	4

a√3		3
	=		k
3		4

a		3
	=		k
√3		4

	3k√3
a =
	4

	9*3√3k2
Pp =
	16*4

	√7
sinα = √1−9/16 = √7/16 =
	4

	H
sinα =
	k

	k√7
H =
	4

teraz dokończ

Marta 22: nie rozumiem dlaczego obliczyłaś "a" w taki sposób który przedstawiłaś

Marta 22: zwracam honor już wiem dobra liczę Twoim sposobem Basiu

Marta 22: ale dodam iż nie chodzi tutaj aby obliczyć wysokośc ostrosłupa tylko Pc czyli PP+PB