w trójkącie równobocznym niula: wewnątrz trójkata równobocznego o boku A wybrano dowolny punkt P . wykaż że suma odległości punktu p od boków tego trójkata jest równa jego wysokości H

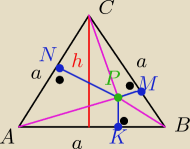
Eta: Przed spaniem podam jeszcze dowód tej zależności: P_ΔABC = P_ΔAPB +P_ΔAPC + P_ΔBPC to: ¹₂a*h= ¹₂a*IPKI + ¹₂a*IPMI + ¹₂a*IPNI ¹₂a*h= ¹₂a( IPKI +IPMI + IPNI) / : ¹₂a zatem h = IPKI + IPMI + IPNI c.b.d.o. Suma tych długości nie zależy od wyboru punktu P i jest zawsze stała i równa długości wysokości tego trójkąta. Miłych snów!, Dobranoc