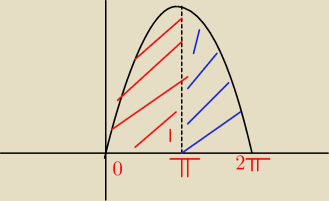
całka oznaczona jok: Oblicz pole od 0 do 2π funkcji f(x) = √1−cosx Po policzeniu ekstremów funkcji wychodzi mi, że peak jest =π oraz są dwa miejsca zerowe 0 oraz 2π,czyli dodaje do siebie 2 pola [0 ; pi] − [pi;0] = 2 pola od 0 do π CO WIDAĆ NA RYSUNKU. Liczę całkę

	√1−t		1
∫√1−cosxdx = ** = ∫		OD 0 DO 2 = ∫
	√1−t*√2−t		√2−t

** t=cosx dt = −sinx granice całkowania: x 0 π t 0 2

jok: niechcąco wcisnąłem wyślij, zaraz dokoncze

Artur_z_miasta_Neptuna: skąd '2' w granicy calkowania skąd taki wynik całki co się stalo z dt = −sinx dx

Artur_z_miasta_Neptuna: napisz mi może jaki wynik Ci wyszedł

jok:

	1
−∫		dt= ** = 2√u w granicach OD 2 DO 0 =− 2√2 * 2 (bo pola) = −
	2−t

4√2. Wynik jest to 4√2, gdzieś zgubilem znak? ** u=2−t du=−dt t 0 2 u 2 0 **

Artur_z_miasta_Neptuna: wynik dobry

jok: aha, to teraz już się wszystko zgadza, dzieki, z tymi dt wiem że ważne

Artur_z_miasta_Neptuna: ale granice całkowania x 0 π t 1 0 przy takim podstawieniu

jok:

	1
−		dt od 1 do 0 = **= 2√u od 1 do 2 = 2*(2√2 − 2} WWTF
	√2−t

** u=2−t du=−dt t 1 0 u 1 2 **

jok: t=cosx dt= −sinx dx sinx = √[1−t]*[2−t]

jok: co jest źle?

jok: już wiem gdzie, gdybym rozpisal sobie to normalnie (zamaist 2 razy pola) to mam 2√2 − 2 +2 − 2√2

jok: po prostu 4√2 wychodzi: D WEEEE