W trójkącie równoramiennym.... Sylwia: W trójkącie równoramiennym ABC kąt przy wierzchołku C jest równy 120°. Symetralne boków trójkąta przecinają się w punkcie E. Wiedząc, że |CE|=4 cm, oblicz obwód trójkąta ABC.

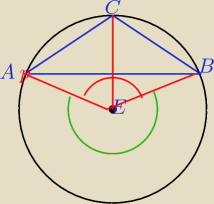
Basia: punkt przecięcia symetralnych to środek okręgu opisanego na trójkącie r = CE = 4 kąt BEA (zielony) = 2*120 = 240 kąt BEA (czerwony) = 360−240 = 120 ⇒ kąty tr.,ACE mają po 60 czyli AC=BC = 4 AB policz np. z tw.sinusów (tr. ACB)

pigor: ... , otóż, np. tak: przy danych miarach kątach, punk E to spodek wysokości CE na AB , zatem z Δ ekierki BEC : |BC|=|AC|=2|CE|=2*4= 8 i |EA|=|EB| , czyli |AB|=2|AE|=2*4√3= 8√3 . więc 2p= |AB|+2|AC|= 8√3+2*8= 8(2+√3)[cm] − szukany obwód ΔABC. ...

Basia: pigor E to nie jest spodek wysokości E to punkt przecięcia symetralnych

Basia: a ponieważ trójkąt jest rozwartokątny E leży na zewnątrz trójkąta

pigor: ..., no tak, nie wiem co sobie ubzdurałem przepraszam, a wszystko co napisałem to bzdety.