Twierdzenie o siecznych i stycznych blan: Częścią wspólną koła k o promieniu 5 i prostej przechodzącej przez punkt A nienależący do koła k jest odcinek KL o długości 7 (punkt L należy do odcinka AK). Wiedząc, że odległość punktu L od punktu A jest równa 9, oblicz odległość środka koła k od punktu A.

blan: ja to robie 5x*x=9*16 ale coś nie wychodzi bo ma być 13 może ja zle to twierdzenie stosuje

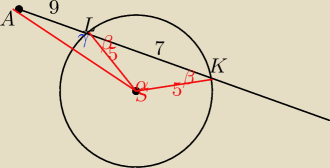
Basia: wyznacz kąt α z tw.cosinusów w tr.KSL

	180−α
β =
	2

γ=180−β z tw. cosinusów w tr.ASL wylicz AS

blan: a własnie czy nie można z twierdzenia siecznych bo tak to to rozumiem ale nie rozumiem z tymi siecznymi bardzo proszę o taki sposób

blan: doszłam do tego ze x*(10+x)=16*9 i wyszło mi żę x=13 lub x=−18 czyli 5+13=28 i mi się nie zgadza ktoś widzi gdzie błąd robie

blan: sory 18

Basia: można; przedłuż AS punkty przecięcia AS z okręgiem B i C wtedy AB*AC = AL*LK x(x+10) = 9*16 x²+10x − 144 = 0 Δ = 100+4*144 = 100+ 576 = 676 √Δ = 26

	−10+26
x1 =		= 8
	2

x₂ < 0 odpada AS = 8+5 = 13

blan: Już to obczaiłam napiszę to żeby ktoś się z tym nie męczył x*(10+x)=16*9 − stosuje twierdzenie o siecznych dalej liczę wychodz x=8 i x =−18 x+r=SA =8+5=13 bez bawienie się i szukania kątów

blan: dzięki Basiu