kwadrat MessiTUjest: wewnatrz kwadratu abcd obrano punkt W taki że trojkat abw jest rownoboczny wyznacz miarę kąta dwc

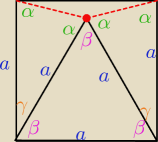
Artur_z_miasta_Neptuna: β = 60⁰ γ+β = 900 −> γ = 30⁰ γ+2α = 180 −> α = 75^o 2α+β+ szukany kąt = 360 → szukany kąt = ....

MessiTUjest: 75 st ?

Artur_z_miasta_Neptuna: no ... raczej nie ... policz jeszcze raz

MessiTUjest: to nie wiem

MessiTUjest: Powiesz jakie jest rozwiaznie ?

Artur_z_miasta_Neptuna: masz wszystko napisane ... wystarczy podstawić co już wczesniej ci wyliczyłem i już masz wynik

MessiTUjest: 210

Artur_z_miasta_Neptuna: cóż ja Ci moge powiedzieć ... nie ... szukany kąt to nie będzie 210^o

MessiTUjest: sorry 150 ?

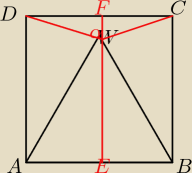
Basia: a − bok kwadratu

	a√3
WE =		bo to jest wysokość tr.równobocznego
	2

	2a−a√3		a(2−√3)
FW = a − WE =		=
	2		2

	DF		a2		1		2+√3
tgα =		=		=		=		= 2+√3
	FW		a(2−√3   ) 2		2−√3		4−3

	2tgα
tg(∡DWC) = tg(2α) =		=
	1−tg2α

2(2+√3)
	=
1−4−4√3−3

2(2+√3)
	=
−6−4√3

2(2+√3)
	=
−2(3+2√3)

	(2+√3)(3−2√3)
−		=
	9 − 4*3

6−4√3+3√3−6
	=
3

	√3
−
	3

czyli ∡DWC = 180−30 = 150 ale może jest jakiś inny, prostszy sposób np. z tw. cosinusów w tr.DAW można wyliczyć DW DW² = a² + a² − 2a*a*cos30

	√3		2−√3
DW2 = 2a2(1−		= 2a2*		= a2(2−√3)
	2		2

i z tw.cosinusów w tr.DWC mamy a² = a²(2−√3)+a²(2−√3) − 2a²(2−√3)*cos(∡DWC) /:a² 1 = 2(2−√3)− 2(2−√3)*cos(∡DWC)

	1−2(2−√3)
cos(∡DWC) =		=
	2(2−√3)

−3+2√3
	=
2(2−√3)

(−3+2√3)(2+√3)
	=
2(4−3)

−6 − 3√3 + 4√3 + 6		√3
	= −
2		2

czyli ∡DWC = 150

Artur_z_miasta_Neptuna: ooo i teraz jest dobrze

Artur_z_miasta_Neptuna: Basiu ... co to za mordowanie ludzi obliczeniami

Basia: no skoro nie można policzyć sumy kątów.............................. a można jeszcze szybciej nawiasem mówiąc

Basia:

	180−30
α =		= 75 ⇒ ∡D=∡C = 90−75 = 15 ⇒ ∡DWC = 180−15−15 = 150
	2