pomozesz? marcin: Napisać równania stycznych do hiperboli 16x² − 9y² = 144 jednakowo odległych od prawego ogniska i od początku układu współrzędnych.

marcin: z tego trzeba skorzystac?

	px		qy
Styczną w punkcie P(p,q) opisujemy wzorem		−		=1
	a2		b2

marcin:

x2		y2
	−		=1 tak?
9		16

imię lub nick: tak, a odległość ogniska od początku układu jest równa √a²+b²

marcin:

	1
czyli		c= √337 hmm beznadziejny wynik?
	2

imię lub nick: hmm, styczna do hiperboli jednakowo odległa od prawego ogniska i początku układu... hmm a² = 9 b²=16 √25=5

marcin: ajj podnioslem jeszcze raz do kwadratu a i b klopsik skorono " jednakowo odległa od prawego ogniska i początku układu" to w punkcie (2,5 ;0) tak? a co dalej jak ta styczne wyznaczyc?

imię lub nick: tak, punkt (2,5;0) jest jednakowo odległy od początku układu i prawego ogniska, ale nie nalezy on do naszej hiperboli.

imię lub nick: jedynie prosta pionowa x=2,5 jest jednakowo odległa od prawego ogniska i początku układu. czyżby taka styczna nie istniała?

marcin: a bo ja myslalem ze to chodiz ze styczne przechodza przez ten punkt ale wlasnie jak moga takie styczne byc jednakowo odlegle,,

imię lub nick: no właśnie też tak myślałem na początku (pierwszy raz rozwiązuje takie zadanie)

marcin: podpowie ktos co z tym fantem zrobic dalej?

Bogdan: Tak, za chwilę

Bogdan:

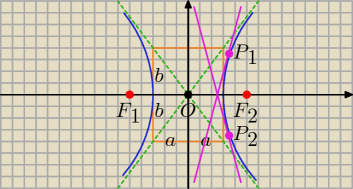
	x2		y2
Hiperbola 16x2 − 9y2 = 144 ⇒		−		= 1
	9		16

Ogniska: F₁ = (−c, 0), F₂ = (c, 0) a² = 9 ⇒ a = 3, b² = 16 ⇒ b = 4, a² + b² = c² ⇒ c = 5 Styczne są położone w jednakowej odległości od punktu O = (0, 0) i F₂ = (5, 0). Punkt styczności P = (x₀, y₀) i zgodnie z warunkami zadania x₀ > 0. Styczna w punkcie P = (x₀, y₀) (różowe linie):

x0		y0
	x −		y = 1 ⇒ 16x0x − 9y0y − 144 = 0,
9		16

A = 16x₀, B = − 9y₀, C = −144. Odległość d₁ stycznej od punktu O = (0, 0):

	|16x0*0 − 9y0*0 − 144|		144
d1 =		=
	√162x02 + 92y02		√162x02 + 92y02

Odległość d₂ stycznej od punktu F₂ = (5, 0)

	|16x0*5−9y0*0−144|		|80x0−144|
d2 =		=
	√162x02+92y02		√162x02+92y02

d₁ = d₂ ⇒ 144 = |80x₀−144| Wyznacz z ostatniego równania x₀, wstaw wyznaczoną wartość x₀ do równania hiperboli 16x² − 9y² = 144 i stąd wyznacz y₀. Otrzymasz dwa punkty styczności: P₁, P₂. Na koniec współrzędne punktów P₁ i P₂ wstaw do równania stycznej:

x0		y0
	x −		y = 1.
9		16

Bogdan: Marcinie, czy wyznaczyłeś x₀ ?

Eta: Marcin poszedł spać Pora i na nas Bogdanie Spokojnej nocy

Bogdan: Brak odpowiedzi. 144 = |80x₀−144| 80x₀−144 = −144 lub 80x₀−144 = 144

	288		18
x0 = 0 lub x0 =		=
	80		5

16*0² − 9y² = 144 sprzeczność.

	18		176		16*11
16*(		)2 − 9y2 = 144 ⇒ y2 =		=
	5		25		25

	4		4
y =		√11 lub y = −		√11
	5		5

	18		4		18		4
P1 = (		,		√11), P2 = (		, −		√11)
	5		5		5		5

	18		1		4		1
Styczna zawierająca punkt P1:		*		x −		√11*		y = 1
	5		9		5		16

2		√11
	x −		y = 1 / *20
5		20

	8		20
8x − √11y − 20 = 0 względnie w postaci kierunkowej: y =		x −
	√11		√11

	18		1		−4		1
Styczna zawierająca punkt P2:		*		x −		√11*		y = 1
	5		9		5		16

2		√11
	x +		y = 1 / *20
5		20

	8		20
8x + √11y − 20 = 0 względnie w postaci kierunkowej: y = −		x +
	√11		√11

	8		20		8		20
Odp.: Styczne: y =		x −		oraz y = −		x +		.
	√11		√11		√11		√11

Dobranoc

Bogdan: Eto, gdy ja byłem uczniem szkoły średniej, to rozwiązywaliśmy takie zadania, nie było żadnego poziomu podstawowego i rozszerzonego, a teraz − szkoda gadać, studenci mają z tym problem. Kolorowych snów

imię lub nick: jednak istnieje taka styczna

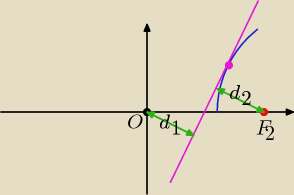
Bogdan: Dzień dobry Marcinie, widzę, że jesteś. Czy przedstawione przeze mnie rozwiązanie jest dla Ciebie zrozumiałe? d₁ = d₂

marcin: omg! nie da sie tego jakos latwiej No nic dzieki wielkie

marcin: wlasnie nie zabardoz wiedzialem gdize te d₁ i d₂ a teraz z tym rysunkiem juz wszystko rozumiem