 Mam takie zadanie:
Trójkąt prostokątny obraca się wokół dłuższej przyprostokątnej. Wiedząc, że pole powierzchni
całkowitej powstałego stożka jest 2√3π razy większe od pola trójkąta, wyznacz miary kątów tego
trójkąta.
Zaczęłam liczyć tak:
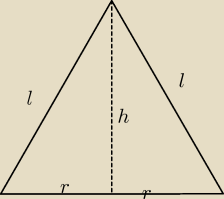
Pc=πr(r+l)
Pt(trójkąta)=0,5*r*h
πr(r+l)=0,5*h*4*π*2√3, czyli po skróceniu:
r+l=h√3
i h=[(r+l)√3]/3
r2+h2=l2
podstawiłam to, ale nic mi nie wychodzi.
Wie ktoś może, co z tym dalej zrobić?
Mam takie zadanie:
Trójkąt prostokątny obraca się wokół dłuższej przyprostokątnej. Wiedząc, że pole powierzchni
całkowitej powstałego stożka jest 2√3π razy większe od pola trójkąta, wyznacz miary kątów tego
trójkąta.
Zaczęłam liczyć tak:
Pc=πr(r+l)
Pt(trójkąta)=0,5*r*h
πr(r+l)=0,5*h*4*π*2√3, czyli po skróceniu:
r+l=h√3
i h=[(r+l)√3]/3
r2+h2=l2
podstawiłam to, ale nic mi nie wychodzi.
Wie ktoś może, co z tym dalej zrobić?
| r | h | ||
+ 1 = | * √3 i zauważmy, że są to odpowiednio cosinus i sinus kąta przy | ||
| l | l |
| 1 | √3 | 1 | 1 | π | √3 | ||||||
cosα − | sinα = − | , zauważamy, że | = sin | i | = | ||||||
| 2 | 2 | 2 | 2 | 6 | 2 |
| π | ||
sin | i chowamy do wzoru na sinus różnicy kątów: | |
| 3 |
| π | 1 | |||
sin( | − α) = − | |||
| 6 | 2 |
| π | ||
A to równanie przy założeniu, że α ∊ (0, | ) potrafisz chyba już rozwiązać | |
| 2 |
 No tak, a ja chciałam sobie utrudnić życie. Dziękuję bardzo
No tak, a ja chciałam sobie utrudnić życie. Dziękuję bardzo 
| 1 | √3 | |||
Sprawdziłem sobie, że sin(30−x)= | cosx − | sinx, bo | ||
| 2 | 2 |
| 1 | √3 | |||
sin(30−x)= sin30cosx−cos30sinx= | cosx − | sinx | ||
| 2 | 2 |

| π | −1 | |||
Jeśli rozwiąże sin( | − α )= | to mam | ||
| 6 | 2 |
| π | −π | π | |||
− α = | α= | ||||
| 6 | 6 | 3 |

 dobre czy złe rozwiązanie podałem (Y/N)
dobre czy złe rozwiązanie podałem (Y/N)