logarytmy Alois~:

	x−1
wyznacz dziedzine funkcji f(x) =log		( x3 −2x2−8x+12)
	x+3

	x−1
{		} −−> mialo byc na dole jako a
	x+3

mam tak:

x−1		x−1
	>0 ∧ {		}≠1 ∧ x3 −2x2−8x+12
x+3		x+3

≠0 x∊(−∞,−3)U(1,+∞) 4≠0 ? czyli że... x≠−3 ∧ x≠2

krystek: x³−2x²−8x+12>0 zapomniałeś dopisać znaku nierówności

Dominik: dobrze to jest przepisane?

krystek: 4≠0 czyli dla każdego x jest spełnione z wyjątkiem x=−3

Alois~: własnie źle ! przepraszam , zagapiłam się już poprawiam

Alois~: x³ −x²−8x+12 o tak być powinno

Alois~: czyli ostatecznie dziedzina to będzie x ∊R − {−3,1,2}

krystek: A nierównośc dla jakich x spełniona?

krystek: x³−x²−8x+12>0 jako liczba logarytmowana.

Alois~: o masz a ja sobie zapisałam zamiast > to ≠ i tak licze... już zaraz poprawiam

Alois~: czyli tutaj chodzi o część wspólną ? (1,+∞) − {2}

krystek: Wszystkie trzy warunki! A gdzie spełniona ostatnia nierównośc , podaj mi

Alois~: ostatnia dla x (−3, +∞) − {2} a ostatecznie mam brać tj wyżej napisałam ?

Mila:

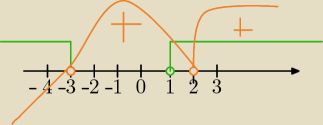
x−1		x−1
	>0 i		≠1 i x3−x2−8x+12>0⇔
x+3		x+3

(x−1)(x+3)>0 i x−1≠x+3 i (x−2)²(x+3)>0 1) x∊(−∞,−3)∪(1,∞) ⋀

	x−1
2) −1≠3 dla każdego x∊R\{−3}⇔		≠1dla każdego x∊R\{−3}
	x+3

⋀ 3) (x−2)²(x+3)>0 na osi zaznaczamy x=2 pierwiastek podwójny ⇔x∊(−3,2)U(2,∞) Część wspólna (1)i (2) i (3) x∊(1,2)U(2,∞)

Alois~: dzięki Mila

Alois~: krystek też dzięki

Mila: właściwie, to podsumowałam Waszą dyskusję.