pomóżcie Wojtek: Wskaż funkcję kwadratową,której zbiorem wartości jest przedział dzóbek zamknięty −2 ∞) A.y=−2x2−do kwadratu i plus 2 By=−(x+1)2−do kwadratu−2 Cy=2(x−1)2−do kwadratu +2 Dy=(x+1)2−do kwadratu −2 jak można to dokładne rozwiązanie

kama: Funkcja kwadratowa −parabola jest zwrocona "do góry nogami" ponieważ wierzchołek paraboli to punkt (p,−2) czyli najmniejszą wartością jest −2. Więc pierwsze dwie odpowiedzi odpadają( współczynnik kierunkowy musi być dodatni. Wystarczy policzyć z funkcji jaki jest wierzchołek D) y=x² +2x −1 przekształcony wzór Δ=8 liczymy deltę q= −Δ/4a= −2 wierzchołek to (p,q)=(p,−2) więc sie zgadza.

Bogdan: Wojtku, zacznij stosować właściwe zapisy, nie pisz y = −2x2, ale y = −2x². Tu obok jest instrukcja zapisywania wyrażeń matematycznych, popatrz na wpisz a otrzymasz i niżej Kliknij po więcej przykładów. kamo, 1. funkcja kwadratowa to nie parabola, 2. gdzie parabola ma głowę, a gdzie nogi? 3. gdzie we wzorze funkcji kwadratowej jest współczynnik kierunkowy ? 4. sformułowanie: jaki jest wierzchołek narzuca pytanie o rodzaje wierzchołków, jakie więc są rodzaje wierzchołków parabol ? 5. co to jest q ?, bo na pewno nie jest to współrzędna wierzchołka paraboli.

wyjaśnienie: funkcja kwadratowa na płaszczyźnie euklidesowej to parabola Ramiona paraboli są skierowane do gory gdy wspołczynnik jst dodatni wspólczynnikiem jest parametr a nie rodzaj wierzchołka a PUNKT na płaszczyźnie liczymy (p,q) q jest drugą współrzędną

Bogdan: Parabola to wykres funkcji kwadratowej, to są jednak różne pojęcia. Właśnie tak powinno się określać położenie ramion paraboli y = ax² + bx + c względem jej wierzchołka, ramiona do góry gdy a > 0, ramiona w dół gdy a < 0. Współczynnik kierunkowy znajduje się we wzorze kierunkowym funkcji liniowej y = ax + b, to współczynnik a. Funkcja kwadratowa nie ma współczynnika kierunkowego. Wierzchołek paraboli to punkt W (x_w, y_w), natomiast liczby p, q to współrzędne wektora [p,q] przesunięcia paraboli.

wyjaśnienie: oznaczenia są względne.

Bogdan: Ale pewien kanon oznaczeń podawany jest w materiale nauczania i w nim x_w, y_w oznaczają współrzędne punktu W, natomiast p, q to współrzędne wektora przesunięcia na układzie współrzędnych figury, np. wykresu funkcji. Lepiej nie wprowadzać zamieszania i niejednoznaczności w tym zakresie.

wyjaśnienie: W takim razie przepraszam, widocznie jestem aż tak stara że leciałam innym "kanonem oznaczeń".

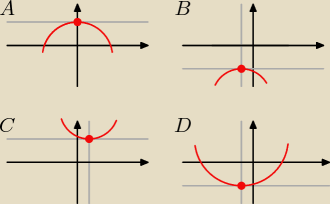
Bogdan: Wróćmy do zadania i zapiszmy je poprawnie. Wskaż funkcję kwadratową,której zbiorem wartości jest przedział <−2, +∞), czyli ZW: y∊<−2, +∞). A. y = −2x² + 2 W = (0, 2) ZW: y∊(−∞, 2> B. y = −(x + 1)² − 2 W = (−1, −2) ZW: y∊(−∞, −2> C. y = 2(x − 1)² + 2 W = (1, 2) ZW: y∊<2, +∞) D. y = (x + 1)² − 2 W = (−1, −2) ZW: y∊ <−2, +∞) Wszystkie wzory podane są w postaci kanonicznej, z której bezpośrednio odczytuje się współrzędne wierzchołka W, monotoniczność funkcji oraz zbiór jej wartości ZW (nie ma potrzeby przekształcać te wzory do postaci ogólnej i potem wyznaczać Δ). Myślę, że teraz widać odpowiedź.